题目内容
15．
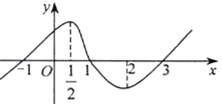已知函数y=f（x）（x∈R）的图象如图所示，f′（x）是f（x）的导函数，则不等式（x-1）f′（x）＜0的解集为（-∞，$\frac{1}{2}$）∪（1，2）．
分析 通过讨论x的符号，根据函数单调性和导数之间的关系即可得到结论．
解答 解：若x-1=0即x=1时，不等式（x-1）•f′（x）＜0不成立．
若x-1＞0即x＞1时，则不等式（x-1）•f′（x）＜0等价为f′（x）＜0，
此时函数单调递减，由图象可知，此时1＜x＜2．
若x-1＜0即x＜1时，则不等式（x-1）•f′（x）＜0等价为f′（x）＞0，
此时函数单调递增，由图象可知，此时x＜$\frac{1}{2}$．，
故不等式x•f′（x）＜0的解集为（-∞，$\frac{1}{2}$）∪（1，2）．
故答案为：（-∞，$\frac{1}{2}$）∪（1，2）．
点评 本题主要考查不等式的解法，利用函数单调性和导数之间的关系即可得到结论．
练习册系列答案
相关题目
10．集合A={x|x（2-x）＞0}，B={x|x-1≥0}，则集合A∪B=（ ）
| A． | {x|1≤x＜2} | B． | {x|x＞2} | C． | {x|x≥1或x＜0} | D． | {x|x＞0} |
4．
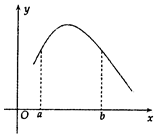函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）
函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）| A． | $f'（{\frac{2ab}{a+b}}）＜f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）$ | B． | $f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{a+b}{2}}）$ | ||
| C． | $f'（{\frac{a+b}{2}}）＜f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）$ | D． | $f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{2ab}{a+b}}）$ |