题目内容
20.已知a+b>0,比较$\frac{a}{{b}^{2}}$+$\frac{b}{{a}^{2}}$与$\frac{1}{a}$+$\frac{1}{b}$的大小.并加以证明.分析 比较法:将两个式子作差变形,通过提取公因式化为完全平方与一个常数的积的形式,判断符号,得出大小关系.
解答 解:$\frac{a}{{b}^{2}}$+$\frac{b}{{a}^{2}}$-$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a-b}{{b}^{2}}$+$\frac{b-a}{{a}^{2}}$=$\frac{(a+b)(a-b)^{2}}{{a}^{2}{b}^{2}}$
∵a+b>0,(a-b)2≥0,
∴$\frac{(a+b)(a-b)^{2}}{{a}^{2}{b}^{2}}$≥0,
∴$\frac{a}{{b}^{2}}$+$\frac{b}{{a}^{2}}$≥$\frac{1}{a}$+$\frac{1}{b}$.
点评 本题考查不等式的证明.用作差的方法比较两个式子的大小,注意将差化为因式积的形式,以便于判断符号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若△ABC内角A、B、C所对的边分别为a、b、c,且${a^2}={c^2}-{b^2}+\sqrt{3}ba$,则∠C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{4}$ |
11.曲线y=$\frac{1}{3}{x^3}$+x-$\frac{1}{3}$在点(1,1)处的切线与坐标轴围成的三角形面积为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.若函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(3-x),x<1}\\{{2}^{x-1},x≥1}\end{array}\right.$,则f(-1)+f(log26)=( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
5.对任意k∈R,直线y=klog2x-2总过一个定点,该定点坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (2,-1) | D. | (-2,-1) |
12.y=4cosx-e|x|图象可能是( )
| A. | 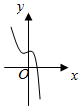 | B. | 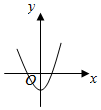 | C. | 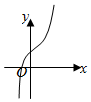 | D. | 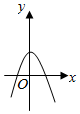 |
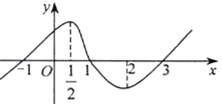 已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).
已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).