题目内容
随机地向曲线y=
与直线y=0所围成的封闭区域内掷一点,则该点与原点所确定的直线的倾斜角小于
的概率为( )
| 4x-x2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意,所求概率是几何概型的概率求法,只要明确基本事件集合的面积,然后求比值.
解答:
解:根据条件,可知曲线是以(2,0)为圆心,2为半径的半圆,
随机地向曲线y=
与直线y=0所围成的封闭区域内掷一点,则该点与原点所确定的直线的倾斜角小于
的概率等于S1与半圆的面积的比,如图,
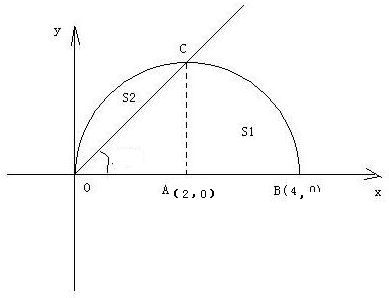
原点与该点的连线与x轴的夹角小于
的点应在S1区域内,
S1的面积和半圆面积的比值即为落在S1内的概率
S1=S△AOC+S扇形ABC=
×2×2+
π×22=2+π,
半圆面积是S半圆=
π22=2π,
由几何概型的公式得P=
=
=
+
.
故选B.
随机地向曲线y=
| 4x-x2 |
| π |
| 4 |

原点与该点的连线与x轴的夹角小于
| π |
| 4 |
S1的面积和半圆面积的比值即为落在S1内的概率
S1=S△AOC+S扇形ABC=
| 1 |
| 2 |
| 1 |
| 4 |
半圆面积是S半圆=
| 1 |
| 2 |
由几何概型的公式得P=
| S1 |
| S半圆 |
| 2+π |
| 2π |
| 1 |
| π |
| 1 |
| 2 |
故选B.
点评:本题考查了几何概型的运用,关键是明确所求概率是基本事件的集合的面积比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
,
是平面上的两个不共线向量,向量
=2
-
,
=m
+3
.若
∥
,则实数m=( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
| A、6 | ||
| B、-6 | ||
| C、3 | ||
D、
|
设m,n是两条不同的直线,α、β是两个不同的平面,则下列结论中正确的是( )
| A、若m⊥α,n∥α,则m⊥n |
| B、若m?α,n?α,则m 与 n 没有公共点 |
| C、若m∥n,m∥α,则n∥α |
| D、若α⊥β,m⊥β,则m∥α |
设F1,F2是椭圆
+
=1的两焦点,M为椭圆上的点,若MF1⊥MF2,则△MF1F2的面积为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、4 | ||
| B、8 | ||
C、4
| ||
D、8
|
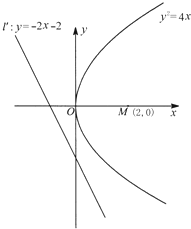 过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.
过点M(2,0)的直线l与抛物线C:y2=4x相交于A,B两点,过点A,B分别作y轴的垂线交直线l′:y=-2x-2于点A′,B′.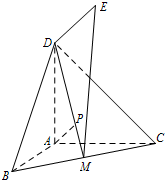 如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.
如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.