Question

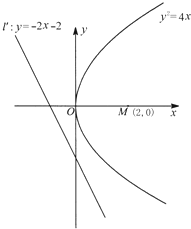过点M（2，0）的直线l与抛物线C：y²=4x相交于A，B两点，过点A，B分别作y轴的垂线交直线l′：y=-2x-2于点A′，B′．
（Ⅰ）若四边形A′B′BA是等腰梯形，求直线l的方程；
（Ⅱ）若A′，O，B，三点共线，求证：AB′与y轴平行；
（Ⅲ）若对于任意一个以AB为直径的圆，在直线x=m上总存在点Q在该圆上，求实数m的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（Ⅰ）若四边形A′B′BA为等腰梯形，则k_AB=2，由此能求出直线l的方程．
（Ⅱ）设直线AB的方程为x=ty+2，A（x₁，y₁），B（x₂，y₂），则A′(-

y1+2

2

，y1)，B′(-

y2+2

2

，y2)，由

x=ty+2 y2=4x

，得y²-4ty-8=0，由此能证明直线AB′与y轴平行．
（Ⅲ）设Q（m，y₀），由已知以AB为直径的圆经过点Q，得k_QA•k_QB=-1，由此推导出16t²-4m²+16m+16mt²+16≥0对一切的t∈R恒成立，由此能求出实数m的取值范围．

解答： （本小题满分15分）
（Ⅰ）解：若四边形A′B′BA为等腰梯形，
则k_AB=2，
故直线l的方程为y=2x-4．…（2分）
（Ⅱ）证明：设直线AB的方程为x=ty+2，A（x₁，y₁），B（x₂，y₂），
则A′(-

y1+2

2

，y1)，B′(-

y2+2

2

，y2)，
由

x=ty+2 y2=4x

，得y²-4ty-8=0，
∴y₁+y₂=4t，y₁y₂═-8．…（4分）
因为A′，O，B三点共线，所以

y2

ty2+2

=

-2y1

y1+2

，…（5分）
即2y₁+y₂=8t+4，又y₁+y₂=4t，得y₂=-4，又y₁y₂=-8，
所以y₁=2，所以A（1，2），B′（1，-4），…（7分）
故直线AB′与y轴平行．…（8分）
（Ⅲ）解：设Q（m，y₀），由已知以AB为直径的圆经过点Q，
得k_QA•k_QB=-1，…（9分）
即

y1-y0

x1-m

•

y2-y0

x2-m

=-1，
即y1y2-y0(y1+y2)+

y

2 0

=-x1x2+m(x1+x2)-m2．（*）
由（Ⅱ）知y₁+y₂=4t，y₁y₂=-8，
则x₁x₂=4，x1+x2=4t2+4，
代入（*）式，得y02-4ty0+m2-4m-4mt2-4=0．…（11分）
因为总存在点Q，所以关于y₀的方程恒有解，所以△≥0要恒成立．
即16t²-4m²+16m+16mt²+16≥0对一切的t∈R恒成立，
整理后得（4m+4）t²≥m²-4m-4．…（12分）
①当m≤-1时，上式不可能对一切的t∈R恒成立；…（13分）
②当m＞-1时，t2≥

m2-4m-4

4m+4

对一切的t∈R恒成立，
只需要m²-4m-4≤0，即2-2

2

≤m≤2+2

2

．…（14分）
综上，所求的实数m的取值范围为[2-2

2

，2+2

2

]． …（15分）

点评：本题考查直线方程的求法，考查直线与y轴平行的证明，考查实数的取值范围的求法，解题时要认真审题，注意函数与方程思想的合理运用．