题目内容
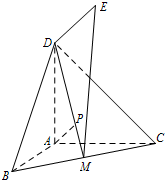 如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.
如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.(Ⅰ)求直线EM与平面BCD所成角的正弦值;
(Ⅱ)P为线段DM上一点,且AP⊥DM,求证:AP∥DE.
考点:直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由ED⊥平面BCD,可得DM为EM在平面BCD上的射影,即∠EMD为EM与平面BCD所成角.解三角形可得直线EM与平面BCD所成角的正弦值;
(Ⅱ)P为线段DM上一点,且AP⊥DM,结合DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.由线面垂直的判定定理,性质定理可得AP∥DE.
(Ⅱ)P为线段DM上一点,且AP⊥DM,结合DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.由线面垂直的判定定理,性质定理可得AP∥DE.
解答:
解:(Ⅰ)∵ED⊥平面BCD,
∴DM为EM在平面BCD上的射影,
∴∠EMD为EM与平面BCD所成角.…(2分)
∵DA⊥平面ABC,AB?平面ABC,AC?平面ABC,
∴DA⊥AB,DA⊥AC,
设DE=DA=AB=AC=a,则DC=DB=
a,
在△ABC中,∠BAC=120°,
∴BC=
a,
又∵M为BC中点,
∴DM⊥BC,BM=
BC=
a,
∴DM=
a.…(5分)
在Rt△EDM中,EM=
=
a,
∴sin∠EMD=
=
=
.…(7分)
(Ⅱ)∵AB=AC,M为BC中点,
∴BC⊥AM.
又DA⊥平面ABC,BC?平面ABC,
∴BC⊥DA,
又∵AM∩DA=A,AM,DA?平面DAM.
∴BC⊥平面DAM.…(9分)
又∵AP?平面DAM,
∴BC⊥AP…(11分)
又AP⊥DM,BC∩DM=M,BC,DM?平面BCD.
∴AP⊥平面BCD …(13分)
又∵ED⊥平面BCD,
∴AP∥DE. …(14分)
∴DM为EM在平面BCD上的射影,
∴∠EMD为EM与平面BCD所成角.…(2分)
∵DA⊥平面ABC,AB?平面ABC,AC?平面ABC,
∴DA⊥AB,DA⊥AC,
设DE=DA=AB=AC=a,则DC=DB=
| 2 |
在△ABC中,∠BAC=120°,
∴BC=
| 3 |
又∵M为BC中点,
∴DM⊥BC,BM=
| 1 |
| 2 |
| ||
| 2 |
∴DM=
| ||
| 2 |
在Rt△EDM中,EM=
| DE 2+DM2 |
| 3 |
| 2 |
∴sin∠EMD=
| DE |
| EM |
| a | ||
|
| 2 |
| 3 |
(Ⅱ)∵AB=AC,M为BC中点,
∴BC⊥AM.
又DA⊥平面ABC,BC?平面ABC,
∴BC⊥DA,
又∵AM∩DA=A,AM,DA?平面DAM.
∴BC⊥平面DAM.…(9分)
又∵AP?平面DAM,
∴BC⊥AP…(11分)
又AP⊥DM,BC∩DM=M,BC,DM?平面BCD.
∴AP⊥平面BCD …(13分)
又∵ED⊥平面BCD,
∴AP∥DE. …(14分)
点评:本题考查的知识点是直线与平面的夹角,直线与平面垂直的判定定理,直线与平面垂直的性质定理,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
随机地向曲线y=
与直线y=0所围成的封闭区域内掷一点,则该点与原点所确定的直线的倾斜角小于
的概率为( )
| 4x-x2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将球的表面积扩大到原来的4倍,则其体积扩大到原来的( )
| A、2倍 | B、4倍 | C、8倍 | D、16倍 |
设F是双曲线
-
=1(a>0,b>0)的左焦点,A(a,b),P是双曲线右支上的动点.若|PF|+|PA|的最小值为3a,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|