题目内容
9.下列命题中正确的个数是( )①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形,其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面,则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据棱柱的定义可得①错误;根据棱锥的定义可得②错误;两个侧面不是相邻的时,侧棱与底面不一定垂直,可得③错误;圆台所有的轴截面是全等的等腰梯形,即④正确,从而得出结论.
解答 解:有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故①错误.
有一个面是多边形,其余各面都是有公共顶点三角形的几何体叫棱锥,故②错误.
当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,如两个侧面不是相邻的时,侧棱与底面不一定垂直,∴③错误;
④圆台所有的轴截面是全等的等腰梯形,正确.
故选A.
点评 本题考查的知识点是棱柱的几何特征,棱锥的几何特征,棱台的几何特征,熟练掌握相关定义是解答的关键,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
20.在平行四边形ABCD中,$\overrightarrow{AB}+\overrightarrow{AD}$=( )
| A. | $\overrightarrow{AC}$ | B. | $\overrightarrow{BD}$ | C. | $\overrightarrow{CA}$ | D. | $\overrightarrow{DB}$ |
17.已知平面α∩平面β=l,直线m?α,且m∩l=P,则( )
| A. | β内必存在直线与m平行,存在直线与m垂直 | |
| B. | β内必不存在直线与m平行,必存在直线与m垂直 | |
| C. | β内必不存在直线与m平行,且不存在直线与m垂直 | |
| D. | β内必存在直线与m平行,不存在直线与m垂直 |
14.$\frac{{tan{{12}°}+tan{{18}°}}}{{1-tan{{12}°}•tan{{18}°}}}$=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
1.若满足x,y约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$,则z=x+y的最大值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | -1 | D. | -3 |
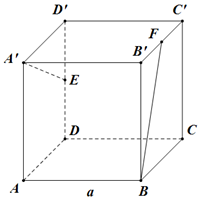 如图正方体ABCD-A′B′C′D′中,E、F为中点,
如图正方体ABCD-A′B′C′D′中,E、F为中点,