题目内容
1．若满足x，y约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$，则z=x+y的最大值为（ ）| A． | $\frac{3}{2}$ | B． | 1 | C． | -1 | D． | -3 |
分析 由约束条件作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．
解答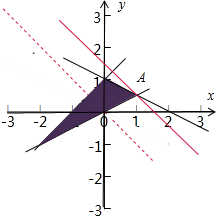 
解：由约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$作出可行域如图，
化目标函数z=x+y为y=-x+z，
由图可知，当直线y=-x+z过A时，目标函数有最大值，
由：$\left\{\begin{array}{l}{x-2y=0}\\{x+2y-2=0}\end{array}\right.$，可得A（1，$\frac{1}{2}$），z的最大值为z=1+$\frac{1}{2}$=$\frac{3}{2}$．
故选：A．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
11．已知倾斜角60°为的直线l平分圆：x2+y2+2x+4y-4=0，则直线l的方程为（ ）
| A． | $\sqrt{3}$x-y+$\sqrt{3}$+2=0 | B． | $\sqrt{3}$x+y+$\sqrt{3}$+2=0 | C． | $\sqrt{3}$x-y+$\sqrt{3}$-2=0 | D． | $\sqrt{3}$x-y-$\sqrt{3}$+2=0 |
9．下列命题中正确的个数是（ ）
①有两个面平行，其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形，其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面，则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形．
①有两个面平行，其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形，其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面，则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．已知函数$y=3sin（ωx+\frac{π}{3}）$的最小正周期为π，将函数$y=3sin（ωx+\frac{π}{3}）$的图象向右平移$\frac{π}{2}$个单位长度，所得图象对应的函数（ ）
| A． | 在区间$[\frac{π}{12}，\frac{7π}{12}]$上单调递减 | B． | 在区间$[\frac{π}{12}，\frac{7π}{12}]$上单调递增 | ||
| C． | 在区间$[-\frac{π}{6}，\frac{π}{3}]$上单调递减 | D． | 在区间$[-\frac{π}{6}，\frac{π}{3}]$上单调递增 |
6．已知不共线的两个向量$\overrightarrow a\;\;，\;\;\overrightarrow b$满足$|{\overrightarrow a-\overrightarrow b}|=3$且$\overrightarrow a⊥（{\overrightarrow a-2\overrightarrow b}）$，则$|{\overrightarrow b}|$=（ ）
| A． | 3 | B． | 4 | C． | $2\sqrt{2}$ | D． | $2\sqrt{3}$ |
13．在如图所示的程序框图中，若输入的m=98，n=63，则输出的结果为（ ）
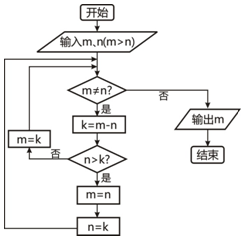
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
10．
一个几何体的三视图如图所示（其中正视图的弧线为四分之一圆周），则该几何体的表面积为（ ）
一个几何体的三视图如图所示（其中正视图的弧线为四分之一圆周），则该几何体的表面积为（ ）| A． | 72+6π | B． | 72+4π | C． | 48+6π | D． | 48+4π |