题目内容
18.从装有红球、白球和黑球各2个的口袋内一次取出2个球,则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球;②两球恰有一白球;③两球至少有一个白球;④两球至多有一个白球”中的哪几个?( )| A. | ①②④ | B. | ①②③ | C. | ①③ | D. | ①② |
分析 结合互斥事件和对立事件的定义,即可得出结论
解答 解:根据题意,结合互斥事件、对立事件的定义可得,事件“两球都为白球”和事件“两球都不是白球”;事件“两球都为白球”和事件“两球中恰有一白球”;不可能同时发生,故它们是互斥事件.
但这两个事件不是对立事件,因为他们的和事件不是必然事件.
故选:D.
点评 本题考查互斥事件与对立事件.首先要求理解互斥事件和对立事件的定义,理解互斥事件与对立事件的联系与区别.同时要能够准确列举某一事件所包含的基本事件,属简单题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
9.下列命题中正确的个数是( )
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形,其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面,则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形.
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形,其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面,则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.已知不共线的两个向量$\overrightarrow a\;\;,\;\;\overrightarrow b$满足$|{\overrightarrow a-\overrightarrow b}|=3$且$\overrightarrow a⊥({\overrightarrow a-2\overrightarrow b})$,则$|{\overrightarrow b}|$=( )
| A. | 3 | B. | 4 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
13.在如图所示的程序框图中,若输入的m=98,n=63,则输出的结果为( )
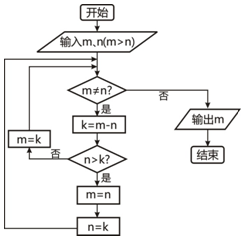

| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
10. 一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为( )
一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为( )
 一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为( )
一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为( )| A. | 72+6π | B. | 72+4π | C. | 48+6π | D. | 48+4π |
7.已知变量x,y满足$\left\{\begin{array}{l}{x^2}-{y^2}≥0\\-k≤x≤k\end{array}\right.$,且目标函数z=x+2y的最小值为-2,则k的值为( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 2 |
8.某环保部门对A,B,C三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如表所示:
已知在这180个数据中随机抽取一个,恰好抽到记录B城市空气质量为优的数据的概率为0.2.
(1)现用分层抽样的方法,从上述180个数据汇总抽取30个进行后续分析,求在C城中应抽取的数据的个数;
(2)已知y≥23,z≥24,求在C城中空气质量为优的天数大于空气质量为良的天数的概率.
| A城 | B城 | C城 | |
| 优(个) | 28 | x | y |
| 良(个) | 32 | 30 | z |
(1)现用分层抽样的方法,从上述180个数据汇总抽取30个进行后续分析,求在C城中应抽取的数据的个数;
(2)已知y≥23,z≥24,求在C城中空气质量为优的天数大于空气质量为良的天数的概率.
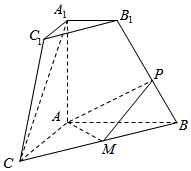 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点.