题目内容
17.已知平面α∩平面β=l,直线m?α,且m∩l=P,则( )| A. | β内必存在直线与m平行,存在直线与m垂直 | |
| B. | β内必不存在直线与m平行,必存在直线与m垂直 | |
| C. | β内必不存在直线与m平行,且不存在直线与m垂直 | |
| D. | β内必存在直线与m平行,不存在直线与m垂直 |
分析 利用面面相交的平面性质,结合直线m的位置关系分别进行讨论判断.
解答 解:因为平面α∩平面β=l,直线m?α,且m∩l=P,
所以在平面内一定存在和m垂直的直线,但不一定存在和直线m平行的直线.
故只有B正确.
故选B.
点评 本题主要考查空间直线和直线平行和垂直的判断,考查学生的空间想象能力.

练习册系列答案
相关题目
9.下列命题中正确的个数是( )
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形,其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面,则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形.
①有两个面平行,其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形,其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面,则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.已知不共线的两个向量$\overrightarrow a\;\;,\;\;\overrightarrow b$满足$|{\overrightarrow a-\overrightarrow b}|=3$且$\overrightarrow a⊥({\overrightarrow a-2\overrightarrow b})$,则$|{\overrightarrow b}|$=( )
| A. | 3 | B. | 4 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
7.已知变量x,y满足$\left\{\begin{array}{l}{x^2}-{y^2}≥0\\-k≤x≤k\end{array}\right.$,且目标函数z=x+2y的最小值为-2,则k的值为( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 2 |
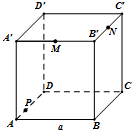 如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.
如图,在棱长为a的正方体ABCD-A′B′C′D′中,M、N分别是棱A′B′、B′C′的中点,P是棱AD上一点,AP=$\frac{a}{3}$,过P、M、N的平面与棱CD交于Q,则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a.