题目内容
19.曲线y=sinx-2x在x=π处的切线方程为3x+y-π=0.分析 求出函数的导数,可得曲线y=sinx-2x在x=π处的切线斜率,求出切点,由点斜式方程可得切线的方程.
解答 解:y=sinx-2x的导数为y′=cosx-2,
可得曲线y=sinx-2x在x=π处的切线斜率为cosπ-2=-3,
切点为(π,-2π),
可得曲线y=sinx-2x在x=π处的切线方程为y-(-2π)=-3(x-π),
即为3x+y-π=0,
故答案为:3x+y-π=0.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
相关题目
18.在如图所示的程序图中,若函数f(x)=$\left\{\begin{array}{l}{{2}^{x},αx≤0}\\{lo{g}_{\frac{1}{2}}x,x>0}\end{array}\right.$,则输出的结果是( )
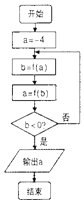

| A. | -3 | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
10.若集合中三个元素为边可构成一个三角形,则该三角形一定不可能是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
14.已知双曲线C与双曲线$\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{48}$=1有相同的渐近线,且与椭圆$\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{169}$=1有相同的焦点,则双曲线C的方程为( )
| A. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
11.已知倾斜角60°为的直线l平分圆:x2+y2+2x+4y-4=0,则直线l的方程为( )
| A. | $\sqrt{3}$x-y+$\sqrt{3}$+2=0 | B. | $\sqrt{3}$x+y+$\sqrt{3}$+2=0 | C. | $\sqrt{3}$x-y+$\sqrt{3}$-2=0 | D. | $\sqrt{3}$x-y-$\sqrt{3}$+2=0 |