题目内容
4．
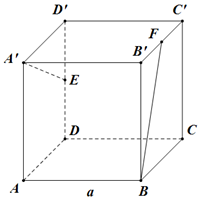如图正方体ABCD-A′B′C′D′中，E、F为中点，（1）AC与A′D′所成角的大小是45°．
（2）AC与A′D 所成角的大小是60°．
（3）A′E与BF所成角的大小是90°．
（本题只需在横线上填上正确的角度即可，无需写出解答过程）
分析 利用平移法，找出异面直线所成角，即可得出结论．
解答 
解：（1）∵A′D′∥AD，∴∠DAC为所求，即AC与A′D′所成角的大小是45°；
（2）A′D∥B′C，∴∠B′CA为所求，即AC与A′D 所成角的大小是60°；
（3）取B′B的中点M，则CM∥A′E，CM⊥BF，∴A′E与BF所成角的大小是90°．
点评 本题考查异面直线所成角，考查学生的计算能力，关键是找出异面直线所成角．
练习册系列答案
相关题目
14．已知双曲线C与双曲线$\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{48}$=1有相同的渐近线，且与椭圆$\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{169}$=1有相同的焦点，则双曲线C的方程为（ ）
| A． | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | B． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C． | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 | D． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
9．下列命题中正确的个数是（ ）
①有两个面平行，其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形，其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面，则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形．
①有两个面平行，其余各面都是平行四边形的几何体叫棱柱
②有一个面是多边形，其余各面都是三角形的几何体叫棱锥
③若有两个侧面垂直于底面，则该四棱柱为直四棱柱
④圆台所有的轴截面是全等的等腰梯形．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．已知函数$y=3sin（ωx+\frac{π}{3}）$的最小正周期为π，将函数$y=3sin（ωx+\frac{π}{3}）$的图象向右平移$\frac{π}{2}$个单位长度，所得图象对应的函数（ ）
| A． | 在区间$[\frac{π}{12}，\frac{7π}{12}]$上单调递减 | B． | 在区间$[\frac{π}{12}，\frac{7π}{12}]$上单调递增 | ||
| C． | 在区间$[-\frac{π}{6}，\frac{π}{3}]$上单调递减 | D． | 在区间$[-\frac{π}{6}，\frac{π}{3}]$上单调递增 |
13．在如图所示的程序框图中，若输入的m=98，n=63，则输出的结果为（ ）
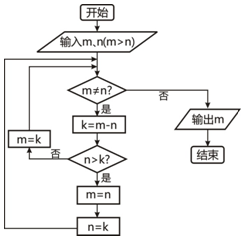
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |