题目内容
已知向量
=(2,1),
=(3,λ),若(2
-
)⊥
,则λ的值为( )
| a |
| b |
| a |
| b |
| b |
| A、3 | B、-1 |
| C、-1或3 | D、-3或1 |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由向量的坐标运算和垂直关系可得λ的方程,解方程可得.
解答:
解:∵向量
=(2,1),
=(3,λ),
∴2
-
=(1,2-λ),
∵(2
-
)⊥
,
∴(2
-
)•
=3×1+λ(2-λ)=0,
解得λ=-1或λ=3
故选:C
| a |
| b |
∴2
| a |
| b |
∵(2
| a |
| b |
| b |
∴(2
| a |
| b |
| b |
解得λ=-1或λ=3
故选:C
点评:本题考查平面向量的数量积与向量的垂直关系,属基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
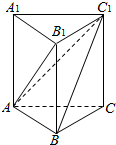 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=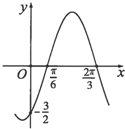 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<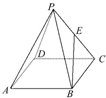 如图所示,正四棱锥P-ABCD的底面积为3,体积为
如图所示,正四棱锥P-ABCD的底面积为3,体积为