题目内容
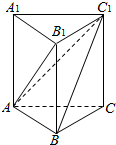 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=| 2 |
(1)求证:BC⊥AB1;
(2)求三棱锥 B1-ABC1的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)证明BC⊥AA1,BC⊥AB,推出BC⊥平面 ABB1A1,然后利用直线与平面垂直的性质定理证明 BC⊥AB1.
(2)直接利用三棱锥的体积与三棱柱的体积关系,转化求解三棱锥的体积即可.
(2)直接利用三棱锥的体积与三棱柱的体积关系,转化求解三棱锥的体积即可.
解答:
(1)证明:∵AA1⊥平面ABC,∴BC⊥AA1,
又∵AB=BC=
,AC=2,
∴AC2=A B2+BC2,
∴BC⊥AB,
而 AA1∩AB=A,且AA1、AB?平面ABB1A1
∴BC⊥平面ABB1A1,
而AB1?平面ABB1A1
故BC⊥AB1.
(2)解:∵VB1-ABC1=VC1-ABB1=
×
S矩形ABB1A1×B1C1=
×
×2×
×
=
.
又∵AB=BC=
| 2 |
∴AC2=A B2+BC2,
∴BC⊥AB,
而 AA1∩AB=A,且AA1、AB?平面ABB1A1
∴BC⊥平面ABB1A1,
而AB1?平面ABB1A1
故BC⊥AB1.
(2)解:∵VB1-ABC1=VC1-ABB1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
点评:本题考查直线与平面垂直的性质定理的应用,几何体的体积的求法,考查计算能力以及逻辑推理能力.

练习册系列答案
相关题目
集合A={x|y=
},B={y|y=log2x,x>0},则A∩B等于( )
| x |
| A、R | B、∅ |
| C、[0,+∞) | D、(0,+∞) |
已知函数f(x)=xcos
,存在f(x)的零点x0,(x0≠0),满足[f′(x0)]2<π2(λ2-x02),则λ的取值范围是( )
| πx |
| λ |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,-
|
设随机变量ξ服从正态分布 N(μ,σ2),若方程x2+4x+ξ=0没有实根的概率是
,则μ=( )
| 1 |
| 2 |
| A、1 | B、2 | C、4 | D、不能确定 |
已知向量
=(2,1),
=(3,λ),若(2
-
)⊥
,则λ的值为( )
| a |
| b |
| a |
| b |
| b |
| A、3 | B、-1 |
| C、-1或3 | D、-3或1 |