题目内容
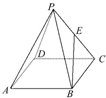 如图所示,正四棱锥P-ABCD的底面积为3,体积为
如图所示,正四棱锥P-ABCD的底面积为3,体积为
| ||
| 2 |
考点:异面直线及其所成的角
专题:空间角
分析:连接AC,BD交于点O,连接OE,PO,则OE∥PA,PA与BE所成的角为∠BEO.由此能求出PA与BE所成的角的大小.
解答:
解:连接AC,BD交于点O,连接OE,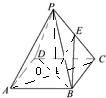 PO,
PO,
∵正四棱锥P-ABCD的底面ABCD是正方形,
∴O是AC中点,又E是PC中点,
∴OE∥PA,∴PA与BE所成的角为∠BEO.
∵正四棱锥P-ABD的底面积为3,体积为
,
∴AB=BC=
,PO=
,AC=
,PA=
,OB=
,
∵OE与PA在同一平面,是三角形PAC的中位线,
则∠OEB即为PA与BE所成的角,
∴OE=
,在Rt△OEB中,tan∠OEB=
=
,
∴∠OEB=
.
故答案为:
.
 PO,
PO,∵正四棱锥P-ABCD的底面ABCD是正方形,
∴O是AC中点,又E是PC中点,
∴OE∥PA,∴PA与BE所成的角为∠BEO.
∵正四棱锥P-ABD的底面积为3,体积为
| ||
| 2 |
∴AB=BC=
| 3 |
| ||
| 2 |
| 6 |
| 2 |
| ||
| 2 |
∵OE与PA在同一平面,是三角形PAC的中位线,
则∠OEB即为PA与BE所成的角,
∴OE=
| ||
| 2 |
| OB |
| OE |
| 3 |
∴∠OEB=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(2,1),
=(3,λ),若(2
-
)⊥
,则λ的值为( )
| a |
| b |
| a |
| b |
| b |
| A、3 | B、-1 |
| C、-1或3 | D、-3或1 |
已知α∈(π,2π),cosα=-
,tan2α=( )
| ||
| 5 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
下列说法不正确的是( )
| A、“若a+b≥2,则a,b中至少有一个不小于1”的逆命题为真 |
| B、存在正实数a,b,使得lg(a+b)=1ga+1gb |
| C、命题p:?x∈R,使得x2+x-1<0,则¬p:?x∈R,使得x2+x-1≥0 |
| D、a+b+c=0是方程ax2+bx+c=0(a≠0)有一个根为1的充分必要条件 |
 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点