题目内容
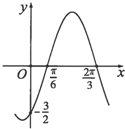 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| 3 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点:y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质
分析:根据三角函数的图象,确定A,ω和φ的值即可得到结论.
解答:
解:由图象知函数的周期T=2(
-
)=π,即
=π,
解得ω=2,
由五点对应法则2×
+φ=0,
解得φ=-
,
则函数f(x)=Asin(2x-
),
∵f(0)=-
,
∴f(0)=Asin(-
)=-
A=-
,
即A=
,
故选:C
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| ω |
解得ω=2,
由五点对应法则2×
| π |
| 6 |
解得φ=-
| π |
| 3 |
则函数f(x)=Asin(2x-
| π |
| 3 |
∵f(0)=-
| 3 |
| 2 |
∴f(0)=Asin(-
| π |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
即A=
| 3 |
故选:C
点评:本题主要考查三角函数解析式的求解,根据条件确定A,ω和φ的值是解决本题的关键.

练习册系列答案
相关题目
用反证法证明命题:“已知a、b∈N+,如果ab可被 5 整除,那么a、b 中至少有一个能被 5 整除”时,假设的内容应为( )
| A、a、b 都能被5 整除 |
| B、a、b 都不能被5 整除 |
| C、a、b 不都能被5 整除 |
| D、a 不能被5 整除 |
已知向量
=(2,1),
=(3,λ),若(2
-
)⊥
,则λ的值为( )
| a |
| b |
| a |
| b |
| b |
| A、3 | B、-1 |
| C、-1或3 | D、-3或1 |
设集合A={x|y=
},B={x|x>a},则“a=0”是“A⊆B”的( )
| x-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点