题目内容
设函数f(x)=
x3+
ax2+2bx+c,f(x)在x=x1处取得极大值,在x=x2处取得极小值,且x1∈(0,1),x2∈(1,2),则
的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
| A、(1,4) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:利用导数研究函数的极值
专题:导数的综合应用,不等式的解法及应用
分析:求导数,利用导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(0,1),x2∈(1,2),得a,b的约束条件,据线性规划求出最值.
解答:
 解:∵函数f(x)=
解:∵函数f(x)=
x3+
ax2+2bx+c,在x=x1处取得极大值,在x=x2处取得极小值,
∴x1,x2是导函数f′(x)=x2+ax+2b的两根
由于导函数f′(x)=x2+ax+2b的图象开口朝上且x1∈(0,1),x2∈(1,2),
∴
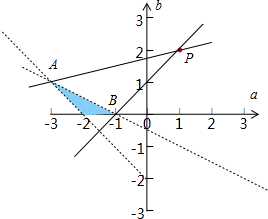
满足条件的约束条件的可行域如图所示:
令Z=
,则其几何意义是区域内的点与P(1,2)连线的斜率,
∴由
,可得a=-1,b=0,B(-1,0).kPB=
=1
,可得a=-3,b=1,可得A(-3,1).kPA=
=
.
∴
∈(
,1).
故选:D.
 解:∵函数f(x)=
解:∵函数f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴x1,x2是导函数f′(x)=x2+ax+2b的两根
由于导函数f′(x)=x2+ax+2b的图象开口朝上且x1∈(0,1),x2∈(1,2),
∴
|
令Z=
| b-2 |
| a-1 |
∴由
|
| 0-2 |
| -1-1 |
|
| 1-2 |
| -3-1 |
| 1 |
| 4 |
∴
| b-2 |
| a-1 |
| 1 |
| 4 |
故选:D.
点评:本题考查函数的导数,函数的极值以及不等式求解函数的最值,考查分析问题解决问题的能力.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
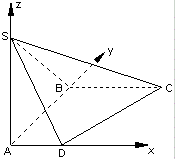 已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= 如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.
如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.