题目内容
求f(x)=3x-7-lnx的极值.
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:先求出导函数,找到导数为0的根,在检验导数为0的根两侧导数的符号即可得出结论.
解答:
解:由题意得函数的定义域是(0,+∞)
f′(x)=3-
=
,
由f′(x)=0得,x=
,
当0<x<
时,f′(x)<0,x>
时,f′(x)>0,
∴当x=
时,f(x)有极小值f(
)=3×
-7-ln
=ln3-6.无极大值.
f′(x)=3-
| 1 |
| x |
| 3x-1 |
| x |
由f′(x)=0得,x=
| 1 |
| 3 |
当0<x<
| 1 |
| 3 |
| 1 |
| 3 |
∴当x=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
从6名志愿者中选出4人,分别从事搜救、医疗、心理辅导、后勤四种不同工作,若其中甲、乙两名志愿者都不能从事心理辅导工作,则不同的选派方案共有( )
| A、96种 | B、180种 |
| C、240种 | D、280种 |
 某城市理论预测2000年到2004年人口总数与年份的关系如下表所示:
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示:

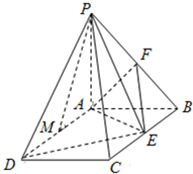 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=