题目内容
2.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$为三个非零平面向量,若$\overrightarrow{p}$=$\frac{\overrightarrow{a}}{\overrightarrow{|a|}}$+$\frac{\overrightarrow{b}}{\overrightarrow{|b|}}$+$\frac{\overrightarrow{c}}{\overrightarrow{|c|}}$,则|$\overrightarrow{p}$|的最大值与最小值之和为( )| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
分析 $\overrightarrow{p}$表示三个单位向量的和,故|$\overrightarrow{p}$|的最大值为3,最小值为0.
解答 解:∵$\frac{\overrightarrow{a}}{\overrightarrow{|a|}}$,$\frac{\overrightarrow{b}}{\overrightarrow{|b|}}$,$\frac{\overrightarrow{c}}{\overrightarrow{|c|}}$为单位向量,∴当$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$方向相同时,|$\overrightarrow{p}$|取得最大值3,当$\frac{\overrightarrow{a}}{\overrightarrow{|a|}}$+$\frac{\overrightarrow{b}}{\overrightarrow{|b|}}$+$\frac{\overrightarrow{c}}{\overrightarrow{|c|}}$=$\overrightarrow{0}$时,|$\overrightarrow{p}$|取得最小值0,
∴|$\overrightarrow{p}$|的最大值与最小值之和是3.
故选:A.
点评 本题考查了平面向量的模长与单位向量的表示方法,是基础题.

练习册系列答案
相关题目
13.函数f(x)=2x2-mx+3在(-∞,2)上的减函数,在(2,+∞)上是增函数,则m的值为( )
| A. | -2 | B. | -8 | C. | 2 | D. | 8 |
10.已知f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若函数y=f[f(x)]-m存在三个零点,则实数m的取值范围是( )
| A. | [0,1] | B. | (0,1] | C. | (-∞,0] | D. | (-∞,0) |
7.已知$\overrightarrow{a}$=(-2,1,3),$\overrightarrow{b}$=(-1,2,1),若$\overrightarrow{a}$⊥($\overrightarrow{a}$-λ$\overrightarrow{b}$),则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
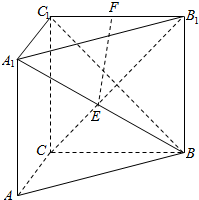 如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.
如图,三棱柱CB=AC=CC1,CB⊥AC,E,F分别是A1B,B1C1的中点,AA1⊥底面ABC.