题目内容
设定义域为R的函数f(x)=
,f(2)=4,f(-3)=f(-1)=1.
(1)求f(x)的解析式;
(2)若关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实数解,求实数m的值.
|
(1)求f(x)的解析式;
(2)若关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实数解,求实数m的值.
考点:分段函数的应用,函数的零点与方程根的关系
专题:计算题,作图题,函数的性质及应用
分析:(1)由题意,f(2)=a=4;f(-3)=9-3b+c=1,f(-1)=1-b+c=1;从而得到a=4,b=4,c=4;从而写出解析式.
(2)作f(x)=
的图象,从而化关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实数解为t2-(2m+1)t+m2=0有两个不同的实数解,且有一个解为1或4;另一个解在(1,4)之间,从而解得.
(2)作f(x)=
|
解答:
解:(1)由题意,f(2)=a=4;
f(-3)=9-3b+c=1,
f(-1)=1-b+c=1;
则a=4,b=4,c=4;
故f(x)=
;
(2)作f(x)=
的图象如下,
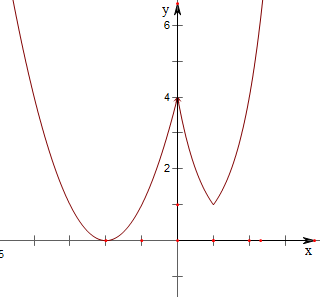
则若使关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实数解,
则t2-(2m+1)t+m2=0有两个不同的实数解,且有一个解为1或4;
若1是t2-(2m+1)t+m2=0得解,
则1-(2m+1)+m2=0;
故m=0或m=2;
若m=0,则t2-(2m+1)t+m2=0的两个解为1,0;不成立;
若m=2,则t2-(2m+1)t+m2=0的两个解为1,4;由图知不成立;
若4是t2-(2m+1)t+m2=0得解,
则16-4(2m+1)+m2=0;
故m=6或m=2;
若m=6,则t2-(2m+1)t+m2=0的两个解为4,9;不成立;
故不存在.
f(-3)=9-3b+c=1,
f(-1)=1-b+c=1;
则a=4,b=4,c=4;
故f(x)=
|
(2)作f(x)=
|

则若使关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实数解,
则t2-(2m+1)t+m2=0有两个不同的实数解,且有一个解为1或4;
若1是t2-(2m+1)t+m2=0得解,
则1-(2m+1)+m2=0;
故m=0或m=2;
若m=0,则t2-(2m+1)t+m2=0的两个解为1,0;不成立;
若m=2,则t2-(2m+1)t+m2=0的两个解为1,4;由图知不成立;
若4是t2-(2m+1)t+m2=0得解,
则16-4(2m+1)+m2=0;
故m=6或m=2;
若m=6,则t2-(2m+1)t+m2=0的两个解为4,9;不成立;
故不存在.
点评:本题考查了分段函数的求法及综合应用,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知F1、F2是双曲线
-
=1(a>b>0)的左右两个焦点,以线段F1F2为直径的圆与双曲线的一条渐近线交于点M,与双曲线交于点N(设M,N均在第一象限),当直线MF1与直线ON平行时,双曲线的离心率取值为e0,则e0所在的区间为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,3) |
已知函数f(x)=
,把函数g(x)=f(x)-
x的偶数零点按从小到大的顺序排列成一个数列,该数列的前n项的和Sn,则S10=( )
|
| 1 |
| 2 |
| A、45 | B、55 | C、90 | D、110 |
函数f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
| A、a≤4 | B、a≤2 |
| C、-4<a≤4 | D、-2≤a≤4 |
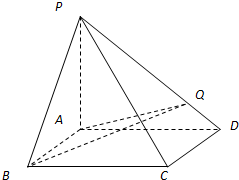 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,已知PA=AD=2AB=4,Q是线段PD上一点,PC⊥AQ.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,已知PA=AD=2AB=4,Q是线段PD上一点,PC⊥AQ. 如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1=4,∠BAC=90°,点D是棱B1C1的中点.