题目内容
已知函数f(x)=
,把函数g(x)=f(x)-
x的偶数零点按从小到大的顺序排列成一个数列,该数列的前n项的和Sn,则S10=( )
|
| 1 |
| 2 |
| A、45 | B、55 | C、90 | D、110 |
考点:数列的求和,分段函数的应用
专题:函数的性质及应用,等差数列与等比数列
分析:由分段函数解析式得到函数f(x)在x>0时的分段解析式,首先求得函数g(x)=f(x)-
x在(-2,0]上的零点,然后根据函数的图象平移得到函数g(x)=f(x)-
x在(0,2],(2,4],(4,6],…,(2n,2n+2]上的零点,得到偶数零点按从小到大的顺序排列的数列,利用等差数列的前n项和得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:当0<x≤2时,有-2<x-2≤0,则f(x)=f(x-2)+1=2x-2,
当2<x≤4时,有0<x-2≤2,则f(x)=f(x-2)+1=2x-4+1,
当4<x≤6时,有2<x-2≤4,则f(x)=f(x-2)+1=2x-6+2,
当6<x≤8时,有4<x-1≤6,则f(x)=f(x-2)+1=2x-8+3,
以此类推,当2n<x≤2n+2(其中n∈N)时,则f(x)=f(x-2)+1=2x-2n-2+n,
∴函数f(x)=2x的图象与直线y=
x+1的交点为:(0,1)和(-1,
),
由于指数函数f(x)=2x为增函数且图象下凸,故它们只有这两个交点.
将函数f(x)=2x和y=
x+1的图象同时向下平移一个单位,即得到函数f(x)=2x-1和y=
x的图象,
取x≤0的部分,可见它们有两个交点(0,0),(-1,-
).
即当x≤0时,方程f(x)-
x=0有两个根x=-1,x=0;
当0<x≤2时,由函数图象平移可得g(x)=f(x)-
x的零点为1,2;
以此类推,函数y=f(x)与y=
x在(2,4],(4,6],…,(2n,2n+2]上的零点分别为:
3,4;5,6;…;2n+1,2n+2;
综上所述函数g(x)=f(x)-
x的偶数零点按从小到大的顺序排列所得数列为:
0,2,4,…,
其通项公式为:an=2(n-1),前10项的和为S10=10×0+
=90.
故选:C.
当2<x≤4时,有0<x-2≤2,则f(x)=f(x-2)+1=2x-4+1,
当4<x≤6时,有2<x-2≤4,则f(x)=f(x-2)+1=2x-6+2,
当6<x≤8时,有4<x-1≤6,则f(x)=f(x-2)+1=2x-8+3,
以此类推,当2n<x≤2n+2(其中n∈N)时,则f(x)=f(x-2)+1=2x-2n-2+n,
∴函数f(x)=2x的图象与直线y=
| 1 |
| 2 |
| 1 |
| 2 |
由于指数函数f(x)=2x为增函数且图象下凸,故它们只有这两个交点.
将函数f(x)=2x和y=
| 1 |
| 2 |
| 1 |
| 2 |
取x≤0的部分,可见它们有两个交点(0,0),(-1,-
| 1 |
| 2 |
即当x≤0时,方程f(x)-
| 1 |
| 2 |
当0<x≤2时,由函数图象平移可得g(x)=f(x)-
| 1 |
| 2 |
以此类推,函数y=f(x)与y=
| 1 |
| 2 |
3,4;5,6;…;2n+1,2n+2;
综上所述函数g(x)=f(x)-
| 1 |
| 2 |
0,2,4,…,
其通项公式为:an=2(n-1),前10项的和为S10=10×0+
| 10×9×2 |
| 2 |
故选:C.
点评:本题考查了分段函数的应用,考查了函数零点的判断方法,考查了等差数列的和的求法,是中档题.

练习册系列答案
相关题目
如果函数f(x)=sin2x+acos2x的图象关于点(
,0)成中心对称,那么a=( )
| π |
| 8 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为-2,两条对称轴间的最短距离为
,直线x=
是其图象的一条对称轴,则符合条件的一个解析式是( )
| π |
| 2 |
| π |
| 6 |
A、y=6sin(2x+
| ||
B、y=6sin(4x+
| ||
C、y=3sin(4x-
| ||
D、y=3sin(2x-
|
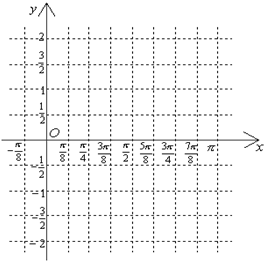 已知曲线f(x)=Asin(ωx+ϕ)+B(A>0,ω>0,|φ|<
已知曲线f(x)=Asin(ωx+ϕ)+B(A>0,ω>0,|φ|<