题目内容
16．若一个三角形具有以下两个性质：（1）三边是连续的三个自然数；（2）最大角是最小角的2倍．则这个三角形的最大边所对角的余弦值为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{1}{8}$ | C． | -$\frac{1}{8}$ | D． | -$\frac{1}{7}$ |
分析 设三角形的三边分别为n-1，n，n+1，对应的角分别为A、B、C，由题意和正弦定理可得cosA=$\frac{n+1}{2（n-1）}$，再由由余弦定理可得cosA=$\frac{n+4}{2（n+1）}$，可得$\frac{n+1}{2（n-1）}$=$\frac{n+4}{2（n+1）}$，解方程可得a值，可得三边长，由余弦定理可得．
解答 解：设三角形的三边分别为n-1，n，n+1，对应的角分别为A、B、C，
则A＜B＜C，由题意可得C=2A，
由正弦定理可得$\frac{n-1}{sinA}$=$\frac{n+1}{sinC}$=$\frac{n+1}{2sinAcosA}$，∴cosA=$\frac{n+1}{2（n-1）}$，
又由余弦定理可得cosA=$\frac{{n}^{2}+（n+1）^{2}-（n-1）^{2}}{2n（n+1）}$=$\frac{n+4}{2（n+1）}$，
∴$\frac{n+1}{2（n-1）}$=$\frac{n+4}{2（n+1）}$，化简可得n2-5n=0解得n=5
∴三角形的三边分别为4，5，6，
∴三角形的最大边所对角的余弦值cosC=$\frac{{4}^{2}+{5}^{2}-{6}^{2}}{2×4×5}$=$\frac{1}{8}$
故选：B．
点评 本题考查解三角形，涉及正余弦定理和三角形的边角关系，属中档题．
练习册系列答案
相关题目
6．在△ABC中，AC=5，BC=6，cos（A-B）=$\frac{37}{40}$，则△ABC面积是（ ）
| A． | 15 | B． | 10$\sqrt{2}$ | C． | 12 | D． | $\frac{3\sqrt{231}}{4}$ |
7．已知集合M={（x，y）|x2+y2≤1}，若实数λ，μ满足：对任意的（x，y）∈M，都有（λx，μy）∈M，则称（λ，μ）是集合M的“和谐实数对”．则以下集合中，存在“和谐实数对”的是（ ）
| A． | {（λ，μ）|λ+μ=4} | B． | {（λ，μ）|λ2+μ2=4} | C． | {（λ，μ）|λ2-4μ=4} | D． | {（λ，μ）|λ2-μ2=4} |
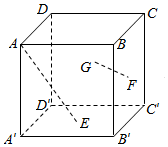在正方体ABCD-A′B′C′D′中，E，F，G分别是面A′C′，面B′C，面CD′的中心，则AE与FG所成的角大小为多少？