题目内容
在数列{an}中,a1=1,a2=3,an+2=3an+1-kan(k≠0)对任意n∈N*成立,令bn=an+1-an,且{bn}是等比数列.
(1)求实数k的值;
(2)求数列{an}的通项公式;
(3)求和:Sn=b1+2b2+3b3+…nbn.
(1)求实数k的值;
(2)求数列{an}的通项公式;
(3)求和:Sn=b1+2b2+3b3+…nbn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件先分别求出a1,a2,a3,a4,进而求出b1,b2,b3,由{bn}成等比数列,由此能求出k.
(2)由已知条件求出bn=2n,根据bn=an+1-an,利用累加法能求出数列{an}的通项公式.
(3)由Sn=b1+2b2+3b3+…nbn=1•2+2•22+3•23+…+n•2n,利用错位相减法能求出Sn.
(2)由已知条件求出bn=2n,根据bn=an+1-an,利用累加法能求出数列{an}的通项公式.
(3)由Sn=b1+2b2+3b3+…nbn=1•2+2•22+3•23+…+n•2n,利用错位相减法能求出Sn.
解答:
解:(1)∵a1=1,a2=3,
a3=3×3-k×1=9-k,
a4=3×(9-k)-k×3=27-6k,
∵bn=an+1-an,
∴b1=3-1=2,b2=6-k,b3=18-5k,
∵{bn}成等比数列,
∴b22=b1•b3,
∴(6-k)2=2×(18-5k),
解得k=2或k=0(舍)
当k=2时,an+2=3an+1-2an,
∴an+2-an+1=2(an+1-an),
∴
=2,∴k=2时满足条件.
(2)∵b1=2,{bn}成等比数列,
=2,∴bn=2n,
∴a2-a1=2,a3-a2=22,…,an-an-1=2n-1,
∴an-a1=1+2+22+23+…+2n-1
=
=2n-1,
∴an=2n.
(3)Sn=b1+2b2+3b3+…nbn
=1•2+2•22+3•23+…+n•2n,①
2Sn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-Sn=2+22+23+…+2n-n×2n+1
=
-n×2n+1
=2n+1-2-n×2n+1,
∴Sn=(n-1)×2n+1+2.
a3=3×3-k×1=9-k,
a4=3×(9-k)-k×3=27-6k,
∵bn=an+1-an,
∴b1=3-1=2,b2=6-k,b3=18-5k,
∵{bn}成等比数列,
∴b22=b1•b3,
∴(6-k)2=2×(18-5k),
解得k=2或k=0(舍)
当k=2时,an+2=3an+1-2an,
∴an+2-an+1=2(an+1-an),
∴
| bn+1 |
| bn |
(2)∵b1=2,{bn}成等比数列,
| bn+1 |
| bn |
∴a2-a1=2,a3-a2=22,…,an-an-1=2n-1,
∴an-a1=1+2+22+23+…+2n-1
=
| 1-2n |
| 1-2 |
∴an=2n.
(3)Sn=b1+2b2+3b3+…nbn
=1•2+2•22+3•23+…+n•2n,①
2Sn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-Sn=2+22+23+…+2n-n×2n+1
=
| 2(1-2n) |
| 1-2 |
=2n+1-2-n×2n+1,
∴Sn=(n-1)×2n+1+2.
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要注意错位相减法的合理运用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
实验测得四组(x,y)的值是(1,2),(2,4),(3,4),(4,5),(5,5),若线性回归方程是
=0.7x+
.则
的值是( )
 |
| y |
 |
| a |
 |
| a |
| A、1.9 | B、1.4 |
| C、2.6 | D、2.2 |
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
| A、(1,-3) | ||||
B、(
| ||||
| C、(3,-3) | ||||
D、(
|
已知异面直线a、b的方向向量分别为
、
,平面α、β的法向量分别为
、
,则下列命题中是假命题的是( )
| a |
| b |
| m |
| n |
A、对于
| ||||||||||||||
B、若
| ||||||||||||||
C、若cos<
| ||||||||||||||
D、若二面角α-l-β的大小为γ,则γ=<
|
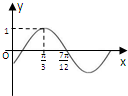 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
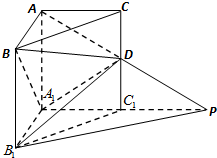 如图,在直三棱柱ABC-A1B1C1中,BC=
如图,在直三棱柱ABC-A1B1C1中,BC=