题目内容
若函数f（x）为偶函数，且
f（x）dx=8，则
[f（x）+2]dx=（ ）
| ∫ | 3 0 |
| ∫ | 3 -3 |
| A、12 | B、16 | C、20 | D、28 |
考点：定积分,函数奇偶性的性质
专题：导数的概念及应用
分析：利用微积分基本定理和偶函数的性质，即可解决，
解答：
解：∵f（x）为偶函数，
∴在y轴两侧的图象对称，y轴两侧对应的曲边梯形面积相等，
∵
[f（x）+2]dx=
f（x）dx+
2dx=2
f（x）dx+2x
=2×8+6-（-6）=28．
故选D．
∴在y轴两侧的图象对称，y轴两侧对应的曲边梯形面积相等，
∵
| ∫ | 3 -3 |
| ∫ | 3 -3 |
| ∫ | 3 -3 |
| ∫ | 3 0 |
| | | 3 -3 |
故选D．
点评：本题考查了定积分，考查了微积分基本定理，是基础题
练习册系列答案
相关题目
关于二项式（x-1）23有下列命题：
①该二项展开式中非常数项的系数和是1；
②该二项展开式中第六项为
x6；
③该二项展开式中系数最大的项是第13项；
④当x=24时，（x-1）23除以24的余数是23．
其中正确命题有（ ）
①该二项展开式中非常数项的系数和是1；
②该二项展开式中第六项为
| C | 6 23 |
③该二项展开式中系数最大的项是第13项；
④当x=24时，（x-1）23除以24的余数是23．
其中正确命题有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知一个空间几何体的三视图如图所示，其中俯视图是边长为6的正三角形，若这个空间几何体存在唯一的一个内切球（与该几何体各个面都相切），则这个几何体的全面积是（ ）A、18
| ||
B、36
| ||
C、45
| ||
D、54
|
在三棱椎P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（ ）
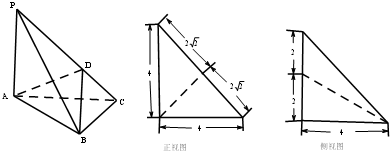
A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|
如图，△ABC的三个内角分别为A，B，C，cosA=