题目内容
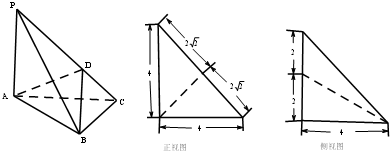
在三棱椎P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )

A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|
考点:直线与平面垂直的判定,命题的真假判断与应用,简单空间图形的三视图
专题:空间位置关系与距离
分析:通过证明直线与平面内的两条相交直线垂直即可证明直线与平面垂直,求出几何体的体积即可.
解答:
解:∵PA⊥平面ABC,∴PA⊥BC,又AC⊥BC,PA∩AC=A,
∴BC⊥平面PAC,
∴BC⊥AD,
又由三视图可得在△PAC中,PA=AC=4,D为PC的中点,
∴AD⊥PC,∴AD⊥平面PBC.
又BC=4,∠ADC=90°,BC⊥平面PAC.
故VD-ABC=VB-ADC=
×
×2
×2
×4=
.
故选:C.
∴BC⊥平面PAC,
∴BC⊥AD,
又由三视图可得在△PAC中,PA=AC=4,D为PC的中点,
∴AD⊥PC,∴AD⊥平面PBC.
又BC=4,∠ADC=90°,BC⊥平面PAC.
故VD-ABC=VB-ADC=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 16 |
| 3 |
故选:C.
点评:本题考查直线与平面垂直的判断,几何体的体积的求法,考查命题的真假的判断与应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知sinα-sinβ=
,cosα-cosβ=
,则cos2
等于( )
| ||
| 3 |
| ||
| 3 |
| α-β |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)的右焦点为F(c,0),直线x=
与一条渐近线交于点A,△OAF的面积为
(O为原点),则抛物线y2=
x的准线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| a2 |
| 2 |
| 4a |
| b |
| A、x=-1 | B、x=-2 |
| C、y=-1 | D、y=-2 |
已知扇形的圆心角为
,它的半径r=3,则该扇形的面积为( )
| π |
| 3 |
| A、3π | ||
B、
| ||
C、
| ||
D、
|
已知A={x|log2x<2},B={x|
<3x<
},则A∩B为( )
| 1 |
| 3 |
| 3 |
A、(0,
| ||
B、(0,
| ||
C、(-1,
| ||
D、(-1,
|
若函数f(x)为偶函数,且
f(x)dx=8,则
[f(x)+2]dx=( )
| ∫ | 3 0 |
| ∫ | 3 -3 |
| A、12 | B、16 | C、20 | D、28 |