题目内容

求直线y=x+1被双曲线x2-
y2
4
=1截得的弦长．
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：联立方程级，求出交点坐标，利用两点间距离公式求解．
解答： 解：直线y=x+1代入双曲线x2-
y2
4
=1，
得4x2-（x+1）2-4=0，
即3x2-2x-5=0，解得
x=-1
y=0
或
x=
5
3
y=
7
3
，
∴直线y=x+1被双曲线x2-
y2
4
=1截得的弦长：
|AB|=
(
5
3
+1)2+(
7
3
-0)2
=
113
3
．
点评：本题考查直线被双曲线截得的弦长的求法，是基础题，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
相关题目
已知函数f（x）=2xlnx．
（1）求单调区间和最小值；
（2）若对x≥1，都有函数f（x）的图象总在直线y=ax-2的上方，求实数a的取值范围．
求值：lg4+lg25+4 
1
2
-（4-π）0．
已知函数f（x）=alnx-ax-3（a∈R）．
（1）若a=-1，求函数f（x）的单调区间；
（2）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，对于任意的t∈[1，2]，函数g（x）=x3+x2[f′（x）+
m
2
]（f′（x）是f（x）的导数）在区间（t，3）上总不是单调函数，求m的取值范围；
（3）求证：
ln2
2
×
ln3
3
×
ln4
4
×…×
lnn
n
＜
1
n
（n≥2，n∈N*）．
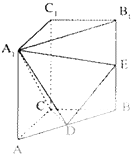直三棱柱ABC-A1B1C1中，AC=CB=AA1=2，∠ACB=90°，E是BB1的中点，D∈AB，∠A1DE=90°．
（1）以C为原点建立坐标系求D点的坐标
（2）求二面角D-A1C-A的大小．
（3）求E到平面 A1CD的距离．
已知等差数列{an}的首项a1=1，公差d＞0，且第二项、第五项、第十四项成等比数列．
（1）求数列{an}的通项公式；
（2）设bn=
1
n(an+3)
 （n∈N*），求数列{bn}的前n项和Sn
（3）在第（2）问的前提下，是否存在最大的整数t，使得对任意的n均有Sn＞
t
36
总成立？若存在，求出t；若不存在，请说明理由．
某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x 2 4 5 6 8
y 30 40 60 50 70
（Ⅰ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（Ⅱ）预测当广告费支出为9百万元时的销售额．
最小二乘法：
?
y
=
?
a
+
?
b
x，
其中
?
b
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
x
2
i
-n
.
x
2
，
?
a
=
.
y
-
?
b
.
x
．
如图，四棱锥P-ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA．
（1）求BC的长；
（2）求异面直线PA与CD所成的角；
（3）求二面角A-BE-D的余弦值．
Sn是等比数列{an}的前n项和，a1=
1
20
，9S3=S6，设Tn=a1a2a3…an，则使Tn取最小值的n值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网