题目内容
已知过曲线C上任意一点P作直线x=-2p(p>0)的垂线,垂足为M,且OP⊥OM.
(1)求曲线C的方程;
(2)设A、B是曲线C上两个不同点,直线OA和OB的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π)时,证明直线AB恒过定点,并求出该定点的坐标.
(1)求曲线C的方程;
(2)设A、B是曲线C上两个不同点,直线OA和OB的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π)时,证明直线AB恒过定点,并求出该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(x,y),则M(-2p,y),由此能求出曲线C的轨迹方程.
(2)设A(x1,y1),B(x2,y2),设直线AB的方程为y=kx+b,x1=
,x2=
,将y=kx+b与y2=2px(p>0),联立得ky2-2py+2pb=0,由此能求出直线AB恒过定点,并求出该定点的坐标.
(2)设A(x1,y1),B(x2,y2),设直线AB的方程为y=kx+b,x1=
| y12 |
| 2p |
| y22 |
| 2p |
解答:
(1)解:设P(x,y),则M(-2p,y),
由OP⊥OM,得
•
=0,
即-2px+y2=0,
所以轨迹方程为y2=2px(x≠0,p>0).
(2)证明:设A(x1,y1),B(x2,y2),
由题意得x1≠x2(否则α+β=π)且x1,x2≠0,
所以直线AB的斜率存在,设其方程为y=kx+b,
x1=
,x2=
,将y=kx+b与y2=2px(p>0),联立消去x,
得ky2-2py+2pb=0,
由韦达定理知y1+y2=
,y1y2=
,①
(i)当θ=
时,即α+β=
时,tanα•tanβ=1,
所以
•
=1,x1x2-y1y2=0,
-y1y1=0,
所以y1y2=-4p2,由①知:
=4p2,
所以b=2pk,因此直线AB的方程可表示为y=k2pk,
即k(x+2P)-y=0,所以直线AB恒过定点(-2p,0).
(Ⅱ)当θ≠
时,由α+β=θ,
得tanθ=tan(α+β)=
=
,
将①式代入上式整理化简得:tanθ=
,
所以b=
+2pk,
此时,直线AB的方程可表示为y=kx+
+2pk.
即k(x+2p)-(y-
)=0.
所以直线AB恒过定点(-2p,
),
所以由(i)(i)知,当θ=
时,直线AB恒过定点(-2p,0),
当θ≠
时直线AB恒过定点(-2p,
).
由OP⊥OM,得
| OP |
| OM |
即-2px+y2=0,
所以轨迹方程为y2=2px(x≠0,p>0).
(2)证明:设A(x1,y1),B(x2,y2),
由题意得x1≠x2(否则α+β=π)且x1,x2≠0,
所以直线AB的斜率存在,设其方程为y=kx+b,
x1=
| y12 |
| 2p |
| y22 |
| 2p |
得ky2-2py+2pb=0,
由韦达定理知y1+y2=
| 2p |
| k |
| 2pb |
| k |
(i)当θ=
| π |
| 2 |
| π |
| 2 |
所以
| y1 |
| x1 |
| y2 |
| x2 |
| y12y22 |
| 4p2 |
所以y1y2=-4p2,由①知:
| 2pb |
| k |
所以b=2pk,因此直线AB的方程可表示为y=k2pk,
即k(x+2P)-y=0,所以直线AB恒过定点(-2p,0).
(Ⅱ)当θ≠
| π |
| 2 |
得tanθ=tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| 2p(y1+y1) |
| y1y2-4p2 |
将①式代入上式整理化简得:tanθ=
| 2p |
| b-2pk |
所以b=
| 2p |
| tanθ |
此时,直线AB的方程可表示为y=kx+
| 2p |
| tanθ |
即k(x+2p)-(y-
| 2p |
| tanθ |
所以直线AB恒过定点(-2p,
| 2p |
| tanθ |
所以由(i)(i)知,当θ=
| π |
| 2 |
当θ≠
| π |
| 2 |
| 29 |
| tanθ |
点评:本题考查曲线方程的求法,考查直线恒过定点的证明,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
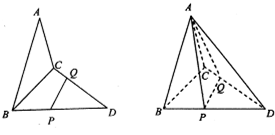 如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合. 如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求
如图所示,等边△ABC的边长为2,以A为圆心,半径为1作圆,PQ是圆的直径,求 “交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示:
“交通指数”是反映道路网畅通或拥堵的概念性指数值.交通指数的取值范围为0至10,分为5个等级:其中[0,2)为畅通,[2,4)为基本畅通,[4,6)为轻度拥堵,[6,8)为中度拥堵,[8,10]为严重拥堵.晚高峰时段,某市交通指挥中心选取了市区60个交通路段,依据其交通指数数据绘制的频数分布表及频率分布直方图如图所示: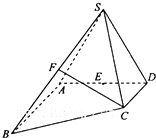 如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=
如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC= 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.