题目内容
如图所示，等边△ABC的边长为2，以A为圆心，半径为1作圆，PQ是圆的直径，求| BP |
| CQ |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由向量的运算可得
•
=1+
•
=1+2cosθ（其中θ为
与
的夹角），然后根据三角形函数求出最值．
| BP |
| CQ |
| AQ |
| BC |
| AQ |
| BC |
解答：
解：
•
=（
+
）•（
+
）
=
•
+
•
+
•
+
•
=2×2×
+
•
+
•
+1×1×（-1）
=1+
•
-
•
=1+
•(
-
)
=1+
•
=1+2cosθ（其中θ为
与
的夹角）
∴θ=0时，
•
的最大值为3，此时四边形BCQP为矩形．
| BP |
| CQ |
| BA |
| AP |
| CA |
| AQ |
=
| BA |
| CA |
| BA |
| AQ |
| AP |
| CA |
| AP |
| AQ |
=2×2×
| 1 |
| 2 |
| BA |
| AQ |
| AP |
| CA |
=1+
| BA |
| AQ |
| AQ |
| CA |
=1+
| AQ |
| BA |
| CA |
=1+
| AQ |
| BC |
=1+2cosθ（其中θ为
| AQ |
| BC |
∴θ=0时，
| BP |
| CQ |
点评：本题考查向量在几何中的应用，以及向量的基本运算，转化是解决问题的关键，属中档题．
练习册系列答案
相关题目
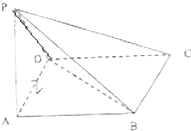如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且AD=
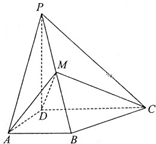如图，四棱锥P-ABCD中，PD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=2，PD=