题目内容
已知数列{Cn}满足Cn=n•2n-2+2n,求数列{Cn}的前n项和Sn.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:利用分组求和法以及错位相减法即可得到结论.
解答:
解:设an=n•2n-2,
则Tn=1•2-1+2•20+3•21+…+n•2n-2,
2Tn=1•20+2•21+3•22+…+n•2n-1,
两式相减得-Tn=1•2-1+20+21+…+2n-2-n•2n-2=
-n•2n-2=2n-1-
-n•2n-2,
则Tn=n•2n-2-2n-1+
,
则Sn=Tn+
×n=n•2n-2-2n-1+
+n(n+1).
则Tn=1•2-1+2•20+3•21+…+n•2n-2,
2Tn=1•20+2•21+3•22+…+n•2n-1,
两式相减得-Tn=1•2-1+20+21+…+2n-2-n•2n-2=
| ||
| 1-2 |
| 1 |
| 2 |
则Tn=n•2n-2-2n-1+
| 1 |
| 2 |
则Sn=Tn+
| (2+2n) |
| 2 |
| 1 |
| 2 |
点评:本题主要考查数列求和,利用分组求和法以及错位相减法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
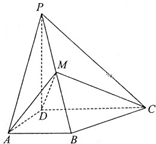 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=

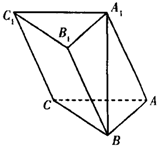 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.