题目内容
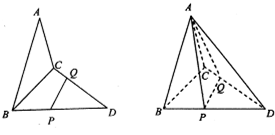 如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求证P为BD的中点;
(Ⅲ)求直线AP与平面ABC所成的角.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)利用线面垂直来证明,∵CQ⊥面ABC,∴CQ⊥AB;
(Ⅱ)设BP=x,在Rt△APO中,AO2+OP2=AP2,得到x的方程求解,进而得到结论;
(Ⅲ)PO⊥面ABC,∴直线AP与平面ABC所成的角就是∠PAO.
(Ⅱ)设BP=x,在Rt△APO中,AO2+OP2=AP2,得到x的方程求解,进而得到结论;
(Ⅲ)PO⊥面ABC,∴直线AP与平面ABC所成的角就是∠PAO.
解答:
证明:(Ⅰ)∵面ABC⊥面BCQ,又CQ⊥BC,∴CQ⊥面ABC,∴CQ⊥AB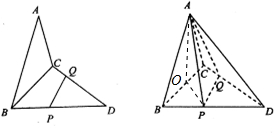
(Ⅱ)作AO⊥BC,垂足为O,则AO⊥面BCQ,连接OP,设AB=1,则BD=2,设BP=x,由题意AP=DP=2-x,在△BPO中,
BO=,∠CBP=45°,∴OP2=x2+(
)2-2×
×cos45°,在Rt△APO中,AO2+OP2=AP2,于是,(
)2+x2+(
)2-2×
×cos45°=(2-x)2
解得x=1,
故P为BD的中点
(Ⅲ)解:由(Ⅰ)知,AO⊥面BCD,P为BD的中点,O为BC的中点,PO⊥面ABC,∴直线AP与平面ABC所成的角就是∠PAO
∠PAO=45°,故直线AP与平面ABC所成的角为45°.

(Ⅱ)作AO⊥BC,垂足为O,则AO⊥面BCQ,连接OP,设AB=1,则BD=2,设BP=x,由题意AP=DP=2-x,在△BPO中,
BO=,∠CBP=45°,∴OP2=x2+(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解得x=1,
故P为BD的中点
(Ⅲ)解:由(Ⅰ)知,AO⊥面BCD,P为BD的中点,O为BC的中点,PO⊥面ABC,∴直线AP与平面ABC所成的角就是∠PAO
∠PAO=45°,故直线AP与平面ABC所成的角为45°.
点评:本题考查线面位置关系,空间距离,线面角,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知变量x,y满足约束条件
,则z=2x+y的最小值为( )
|
| A、0 | B、1 | C、4 | D、6 |
圆锥的底面半径为1,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | ||||
| B、5π | ||||
| C、3π | ||||
D、
|
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD= 如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.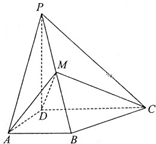 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=