题目内容
求函数y=(cosx-
)2+2在x∈[
,
π]的值域,并写出取得最值时的x的取值集合.
| 1 |
| 2 |
| π |
| 3 |
| 2 |
| 3 |
考点:函数的值域
专题:三角函数的图像与性质
分析:利用换元法令t=cosx,由于x∈[
,
π],则t∈[-
,
],转化成关于t的二次函数z在闭区间上求值域即可.
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:令t=cosx,由于x∈[
,
π],则t∈[-
,
],
则y=(t-
)2+2,t∈[-
,
]
由于y=(t-
)2+2在[-
,
]上为减函数,
所以函数的值域为:[2,3],
当t=-
,即cosx=-
,即x=
π,ymax=3;
当t=
,即cosx=
,即x=
,ymin=2.
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
则y=(t-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于y=(t-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以函数的值域为:[2,3],
当t=-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
当t=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
点评:本题主要考查了函数的值域,以及余弦函数的单调性等有关知识,属于基础题.

练习册系列答案
相关题目
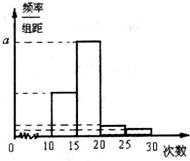 对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: