题目内容
在圆C:x2+y2-2x-2y-7=0上总有四个点到直线l:3x+4y+m=0的距离是1,则实数m的取值范围是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:圆方程化为标准方程,利用圆x2+y2-2x-2y-7=0上总有四个点到直线l:3x+4y+m=0的距离是1,可得圆心到直线的距离小于2,即可求得实数m的取值范围.
解答:
解:圆x2+y2-2x-2y-7=0可化为(x-1)2+(y-1)2=9,圆心(1,1),半径为3.
∵圆x2+y2-2x-2y-7=0上有四点到直线l:3x+4y+m=0的距离为1,
∴
<2
∴-17<m<3
故答案为:(-17,3).
∵圆x2+y2-2x-2y-7=0上有四点到直线l:3x+4y+m=0的距离为1,
∴
| |3+4+m| | ||
|
∴-17<m<3
故答案为:(-17,3).
点评:本题考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知l,m为不同的直线,α,β为不同的平面,如果l?α,且m?β,那么下列命题中不正确的是( )
| A、“l⊥β”是“α⊥β”的充分不必要条件 |
| B、“l⊥m”是“l⊥β”的必要不充分条件 |
| C、“m∥α”是“l∥m”的充要条件 |
| D、“l⊥m”是“α⊥β”的既不充分也不必要条件 |
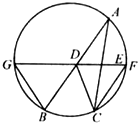 如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交于△ABC的外接圆于F,G两点,若BC=2EF,证明: