题目内容

已知|
a
|=2，|
b
|=2
2
，|
c
|=2
3
，且
a
+
b
+
c
=
0
，则
a
•
b
+
b
•
c
+
a
•
c
=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：把
a
+
b
+
c
=
0
两边平方，变形可得
a
•
b
+
b
•
c
+
a
•
c
=-
1
2
（
a
2+
b
2+
c
2），代入数据计算可得．
解答： 解：∵
a
+
b
+
c
=
0
，∴平方可得（
a
+
b
+
c
）2=
0
2，
∴
a
2+
b
2+
c
2+2（
a
•
b
+
b
•
c
+
a
•
c
）=0，
∴
a
•
b
+
b
•
c
+
a
•
c
=-
1
2
（
a
2+
b
2+
c
2）
=-
1
2
（4+8+12）=-12
故答案为：-12
点评：本题考查平面向量数量积的运算，由
a
+
b
+
c
=
0
两边平方是解决问题的关键，属中档题．
练习册系列答案
相关题目
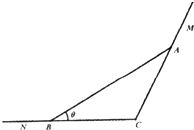如图，用木板AB借助墙角MCN转成一个三角形ABC区域，用以堆放谷物，已知∠MCN=
2
3
π，AB=
3
．
（Ⅰ）若AC=x，BC=y，试写出一个关于变量x，y的方程；
（Ⅱ）若∠ABC=θ，试用θ表示△ABC的面积f（θ），并将f（θ）化简为Asin（ωx+φ）+b的形式；
（Ⅲ）请你利用（Ⅰ）（Ⅱ）中的一个结论，求出△ABC面积的最大值．
若对满足不等式组
y≥1
y≤2x
2x+3y≤12
的任意实数x，y，都有2x+y≥k成立，则实数k的最大值为
 
．
若函数f（x）=x2cos2θ-4xsinθ+12对一切实数x均有f（x）＞0成立，若0＜θ＜π，则θ的取值范围是
 
．
在圆C：x2+y2-2x-2y-7=0上总有四个点到直线l：3x+4y+m=0的距离是1，则实数m的取值范围是
 
．
已知菱形ABCD的边长为a，∠DAB=60°，
EC
=2
DE
，则
AE
•
DB
的值为
 
．
二项式（x+
1
x
）5的展开式中含x3的项的系数是
 
（用数字作答）．
已知函数f（x）=ex-e-x，实数x，y满足f（x2-2x）+f（2y-y2）≥0，若点M（1，2），N（x，y），则当1≤x≤4时，
OM
•
ON
的最大值为
 
（其中O为坐标原点）
已知程序框图如图所示，输入x的值为7时，输出y的值为（　　）
A、
1
2
B、
1
4
C、
1
8
D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网