题目内容
已知两个单位向量
，
的夹角为30°，
=t
+
，
=
-t
．若
•
=0，则正实数t= ．
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义，求得向量a，b的数量积，再由向量垂直的条件：数量积为0，结合向量的平方即为模的平方，计算即可得到t．
解答：
解：两个单位向量
，
的夹角为30°，
则
•
=1×1×cos30°=
，
由
=t
+
，
=
-t
，
若
•
=0，则（t
+
）•（
-t
）=0，
即有t
2-t
2+（1-t2）
•
=0，
则
（1-t2）=0，
解得，t=1（-1舍去）．
故答案为：1．
| a |
| b |
则
| a |
| b |
| ||
| 2 |
由
| c |
| a |
| b |
| d |
| a |
| b |
若
| c |
| d |
| a |
| b |
| a |
| b |
即有t
| a |
| b |
| a |
| b |
则
| ||
| 2 |
解得，t=1（-1舍去）．
故答案为：1．
点评：本题考查平面向量的数量积的定义和性质，考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
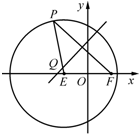如图，已知圆E：