题目内容
20.(1)若$sinα=-\frac{5}{13}$,求tanα;(2)若tanα=2,求sin2α+2sinαcosα的值.
分析 (1)由$sinα=-\frac{5}{13},{sin^2}α+{cos^2}α=1$,即可得解${cos^2}α=\frac{144}{169}$,讨论α的范围,确定三角函数值的符号,利用同角三角函数基本关系式即可求值.
(2)原式分母用1=sin2α+cos2α代替,再利用同角三角函数基本关系式即可得解.
解答 解:(1)∵$sinα=-\frac{5}{13},{sin^2}α+{cos^2}α=1$,
∴${cos^2}α=\frac{144}{169}$,
若α第三象限角,则$cosα=-\frac{12}{13},tanα=\frac{sinα}{cosα}=\frac{5}{12}$,
若α第四象限角,则$cosα=\frac{12}{13},tanα=\frac{sinα}{cosα}=-\frac{5}{12}$.
(2)${sin^2}α+2sinαcosα=\frac{{{{sin}^2}α+2sinαcosα}}{{{{sin}^2}α+{{cos}^2}α}}=\frac{{{{tan}^2}α+2tanα}}{{{{tan}^2}α+1}}=\frac{8}{5}$.
点评 本题主要考查了同角三角函数基本关系式的应用,考查了计算能力和转化思想、分类讨论思想的应用,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
8.下列集合与{x|x2-x=0}相等的是( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {1,2} |
11.已知$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=2$,且$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$,则$\overrightarrow a•\overrightarrow b$=( )
| A. | 6 | B. | 3 | C. | $3\sqrt{3}$ | D. | $2\sqrt{3}$ |
8.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|3x+4y≤12,x≥0,y≥0},若向区域Ω内随机投一点P,则点P落在区域A内的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
5.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.
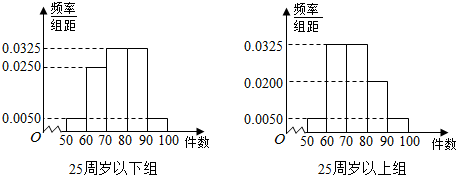
规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
附表:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)

规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
附表:
| P(K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
12.已知$\overrightarrow{a}$=5$\overrightarrow{e}$,$\overrightarrow{b}$=-3$\overrightarrow{e}$,$\overrightarrow{c}$=4$\overrightarrow{e}$,则2$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$=( )
| A. | 5$\overrightarrow{e}$ | B. | -5$\overrightarrow{e}$ | C. | 23$\overrightarrow{e}$ | D. | -23$\overrightarrow{e}$ |