题目内容
15．实数x，y满足y=2x2-4x+1，（0≤x≤1），则$\frac{y-2}{x-2}$的最大值为（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 先将函数化简，再利用换元法，进而可确定函数在定义域内为单调增函数，从而可求函数的最大值．
解答 解：∵y=2x2-4x+1，（0≤x≤1），
∴$\frac{y-2}{x-2}$=$\frac{2{x}^{2}-4x-1}{x-2}$
令x-2=t（-2≤t≤-1），则x=t+2
∴$\frac{y-2}{x-2}$=$\frac{{2t}^{2}+4t-1}{t}$=2t+4-$\frac{1}{t}$，
设f（t）=2t-$\frac{1}{t}$+4，f′（t）=2+$\frac{1}{{t}^{2}}$＞0，
∴函数在[-2，-1]上，函数为增函数
∴t=-1时，函数取得最大值f（-1）=3；
故选：B．
点评 本题重点考查函数的最值，考查函数的单调性，考查换元法的使用，有一定的综合性．
练习册系列答案
相关题目
3．函数f（x）=2sin（ωx+$\frac{π}{4}$）（ω＞0）与函数g（x）=cos（ωx+φ）（|φ|＜$\frac{π}{2}$）的对称轴完全相同，则φ=（ ）
| A． | -$\frac{π}{4}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | -$\frac{π}{2}$ |
3．命题“若x=2，则x＞1”的逆否命题是（ ）
| A． | 若x＞1，则x=2 | B． | 若x=2，则x≤1 | C． | 若x≠2，则x≤1 | D． | 若x≤1，则x≠2 |
10．
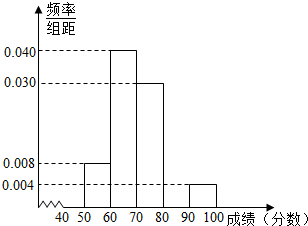学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．
（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
（Ⅲ）现从分数在[80，90），[90，100]的9名同学中随机抽取两名同学，求被抽取的两名学生分数均不低于90分的概率．
学校从参加高二年级期末考试的学生中抽出一些学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），所得数据整理后，列出了如下频率分布表．（Ⅰ）在给出的样本频率分布表中，求A，B，C的值；
（Ⅱ）补全频率分布直方图，并利用它估计全体高二年级学生期末数学成绩的众数、中位数；
| 分组 | 频数 | 频率 |
| [40，50） | A | 0.04 |
| [50，60） | 4 | 0.08 |
| [60，70） | 20 | 0.40 |
| [70，80） | 15 | 0.30 |
| [80，90） | 7 | B |
| [90，100] | 2 | 0.04 |
| 合计 | C | 1 |
7．定积分$\int_1^e{（2x+\frac{1}{x}）}dx$的值为（ ）
| A． | e2-1 | B． | e2 | C． | e2+1 | D． | e2+2 |
4．在四面体ABCD中，E，F分别是棱BC，AD的中点，设$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AC}$=$\overrightarrow b$，$\overrightarrow{AD}$=$\overrightarrow c$，且$\overrightarrow{EF}$=$x\overrightarrow a+y\overrightarrow b+z\overrightarrow c$，则x，y，z的值分别为（ ）
| A． | $-\frac{1}{2}，-\frac{1}{2}，\frac{1}{2}$ | B． | $-\frac{1}{2}，\frac{1}{2}，-\frac{1}{2}$ | C． | $\frac{1}{2}，\frac{1}{2}，-\frac{1}{2}$ | D． | $\frac{1}{2}，-\frac{1}{2}，\frac{1}{2}$ |