题目内容
8.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|3x+4y≤12,x≥0,y≥0},若向区域Ω内随机投一点P,则点P落在区域A内的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 画出Ω与A表示的平面区域,求出对应面积的比即可.
解答  解:画出Ω={(x,y)|x+y≤6,x≥0,y≥0}和A={(x,y)|3x+4y≤12,x≥0,y≥0}表示的平面区域,如图所示;
解:画出Ω={(x,y)|x+y≤6,x≥0,y≥0}和A={(x,y)|3x+4y≤12,x≥0,y≥0}表示的平面区域,如图所示;
则区域Ω表示的平面区域面积是$\frac{1}{2}$×62=18,
区域A(阴影)的面积为$\frac{1}{2}$×3×4=6,
所求的概率为P=$\frac{6}{18}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了几何概型的求法问题,也考查了二元一次不等式表示平面区域的应用问题,是基础题目.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
16.下列判断中不正确的是( )
| A. | r为变量间的相关系数,|r|值越大,线性相关程度越高 | |
| B. | 在平面直角坐标系中,可以用散点图发现变量之间的变化规律 | |
| C. | 线性回归方程代表了观测值x、y之间的关系 | |
| D. | 任何一组观测值都能得到具有代表意义的回归直线方程 |
3.命题“若x=2,则x>1”的逆否命题是( )
| A. | 若x>1,则x=2 | B. | 若x=2,则x≤1 | C. | 若x≠2,则x≤1 | D. | 若x≤1,则x≠2 |
13.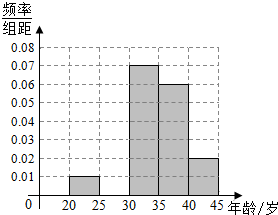 由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》,某部门从参加创作的507名画师中随机抽出100名画师,得到画师年龄的频率分布表如下表所示.
由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》,某部门从参加创作的507名画师中随机抽出100名画师,得到画师年龄的频率分布表如下表所示.
(Ⅰ)求a,b的值;并补全频率分布直方图;
(Ⅱ)根据频率分布直方图估计这507名画师年龄的平均数;
(Ⅲ)在抽出的[20,25)岁的5名画师中有3名男画师,2名女画师.在这5名画师中任选两人去参加某绘画比赛,选出的恰好是一男一女的概率是多少?
 由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》,某部门从参加创作的507名画师中随机抽出100名画师,得到画师年龄的频率分布表如下表所示.
由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》,某部门从参加创作的507名画师中随机抽出100名画师,得到画师年龄的频率分布表如下表所示.(Ⅰ)求a,b的值;并补全频率分布直方图;
(Ⅱ)根据频率分布直方图估计这507名画师年龄的平均数;
(Ⅲ)在抽出的[20,25)岁的5名画师中有3名男画师,2名女画师.在这5名画师中任选两人去参加某绘画比赛,选出的恰好是一男一女的概率是多少?
| 分组(岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | a | 0.200 |
| [30,35) | 35 | b |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
17.设$a={0.3^{\frac{1}{2}}},b={0.4^{\frac{1}{2}}},c={log_3}0.6$,则( )
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | a<b<c |
 已知函数f(x)=Asin(ωx+$\frac{π}{3}$)(A>0,ω>0)的部分图象如图所示.
已知函数f(x)=Asin(ωx+$\frac{π}{3}$)(A>0,ω>0)的部分图象如图所示.