题目内容

3．设f（x）是以2为周期的奇函数，且f（-$\frac{2}{5}$）=3，若sinα=$\frac{\sqrt{5}}{5}$，则f（4cos2α）的值等于-3．

分析 根据sinα=$\frac{\sqrt{5}}{5}$求出4cos2α，根据f（x）的周期性和奇偶性得出答案．

解答 解：cos2α=1-2sin2α=$\frac{3}{5}$，∴4cos2α=$\frac{12}{5}$．
∴f（4cos2α）=f（$\frac{12}{5}$）=f（$\frac{12}{5}$-2）=f（$\frac{2}{5}$）=-f（-$\frac{2}{5}$）=-3．
故答案为-3．

点评 本题考查了三角函数化简求值，函数周期性与奇偶性的应用，属于基础题．

练习册系列答案
相关题目
10．直线l垂直于直线y=x+1，原点O到l的距离为1，且l与y轴正半轴有交点，则直线l的方程是（　　）
A．x+y-$\sqrt{2}$=0B．x+y+1=0C．x+y-1=0D．x+y+$\sqrt{2}$=0
14．如图为一几何体的三视图，其中这三个视图完全一样，则该几何体的表面积为（　　）
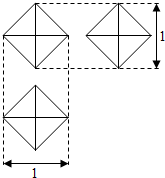
A．$\sqrt{3}$B．2$\sqrt{2}$C．4D．6
11．执行如图所示的程序框图，如果输入的x，t均为2，则输出的M等于（　　）
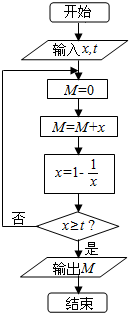
A．$\frac{1}{2}$B．$\frac{3}{2}$C．$\frac{5}{2}$D．$\frac{7}{2}$
18．已知点A（1，-2，2），B（2，-2，-1），C（6，5，2），O为坐标原点，则三棱锥O-ABC的体积为（　　）
A．$\frac{65}{3}$B．$\frac{\sqrt{65}}{3}$C．$\frac{\sqrt{65}}{6}$D．$\frac{65}{6}$
8．设函数f（x）=lnx+x2-2ax+a2，a属于R．
（1）讨论函数f（x）极值点的情况；
（2）若函数f（x）在[$\frac{1}{2}$，2]上不是单调函数．试求实数a的取值范围．
15．已知椭圆$\frac{x^2}{2}$+y2=1与直线y=x+m交于A、B两点，且|AB|=$\frac{4\sqrt{2}}{3}$，则实数m的值为（　　）
A．±1B．±$\frac{1}{2}$C．$\sqrt{2}$D．±$\sqrt{2}$
12．化简：（-3a${\;}^{\frac{1}{3}}$•b${\;}^{\frac{2}{3}}$）（a${\;}^{\frac{1}{2}}$•b${\;}^{\frac{1}{2}}$）÷（-2a${\;}^{\frac{5}{6}}$•b${\;}^{\frac{1}{6}}$）=$\frac{3}{2}b$．
13．设集合A={x|x2-2x≥0}，集合B={x|2x＞1}，则A∩B=（　　）
A．（0，2]B．[0，2]C．[2，+∞）D．（2，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网