题目内容
11．执行如图所示的程序框图，如果输入的x，t均为2，则输出的M等于（ ）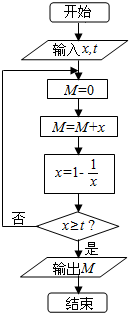
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |
分析 根据条件，依次运行程序，即可得到结论．
解答 解：当x=2时，M=2，1-$\frac{1}{x}$=$\frac{1}{2}$＜2；
x=$\frac{1}{2}$，M=$\frac{5}{2}$，1-$\frac{1}{x}$=-1＜2；
x=-1，M=$\frac{3}{2}$，1-$\frac{1}{x}$=2≥2；
程序结束．输出M=$\frac{3}{2}$，
故选：B．
点评 本题主要考查程序框图的识别和判断，比较基础．
练习册系列答案
期末集结号系列答案
相关题目
18．已知tanα，tanβ是方程6x2-5x+1=0两个根且0＜α＜$\frac{π}{2}$，π＜β＜$\frac{3π}{2}$，则α+β的值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{4}$ | C． | $\frac{5π}{4}$ | D． | $\frac{7π}{4}$ |
2．已知f（$\frac{x+1}{x}$）=$\frac{2x+1}{{x}^{2}}$，则（ ）
| A． | f（x）=x2+1（x≠0） | B． | f（x）=x2+1（x≠1） | C． | f（x）=x2-1（x≠1） | D． | f（x）=x2-1（x≠0） |
如图，在四棱锥P-ABCD中，PA垂直于底面ABCD，底面ABCD是边长为2的菱形，且∠ABC=45°，PA=AB，则直线AP与平面PBC所成的角的正切值是$\frac{\sqrt{2}}{2}$．
1．
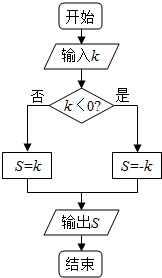直线l斜率为$\frac{1}{2}$，倾斜角为α，将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k，则将k值执行如图所示程序后，输出S值为（ ）
直线l斜率为$\frac{1}{2}$，倾斜角为α，将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k，则将k值执行如图所示程序后，输出S值为（ ）| A． | $\frac{4}{3}$ | B． | -$\frac{4}{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |