题目内容
18.已知点A(1,-2,2),B(2,-2,-1),C(6,5,2),O为坐标原点,则三棱锥O-ABC的体积为( )| A. | $\frac{65}{3}$ | B. | $\frac{\sqrt{65}}{3}$ | C. | $\frac{\sqrt{65}}{6}$ | D. | $\frac{65}{6}$ |
分析 使用向量求出△ABC的面积,O到平面ABC的距离,代入体积公式计算.
解答 解:$\overrightarrow{AB}$=(1,0,-3),$\overrightarrow{AC}$=(5,7,0),∴$\overrightarrow{AB}•\overrightarrow{AC}$=5.|$\overrightarrow{AB}$|=$\sqrt{10}$,|$\overrightarrow{AC}$|=$\sqrt{74}$.
∴cos<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}|•|\overrightarrow{AC}|}$=$\frac{5}{\sqrt{740}}$.∴sin<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{\sqrt{715}}{\sqrt{740}}$.
∴S△ABC=$\frac{1}{2}$AB•AC•sin<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{\sqrt{715}}{2}$.
设平面ABC的法向量为$\overrightarrow{n}$(x,y,z),则$\overrightarrow{n}⊥\overrightarrow{AB}$,$\overrightarrow{n}⊥\overrightarrow{AC}$,
∴$\left\{\begin{array}{l}{x-3z=0}\\{5x+7y=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=(3,-$\frac{15}{7}$,1).∴|$\overrightarrow{n}$|=$\frac{\sqrt{715}}{7}$.
$\overrightarrow{OA}$=(1,-2,2),$\overrightarrow{n}•\overrightarrow{OA}$=$\frac{65}{7}$.
∴点O到平面ABC的距离d=$\frac{\overrightarrow{n}•\overrightarrow{OA}}{|\overrightarrow{n}|}$=$\frac{65}{\sqrt{715}}$.
∴V=$\frac{1}{3}$•S△BCD•d=$\frac{1}{3}×$$\frac{\sqrt{715}}{2}$×$\frac{65}{\sqrt{715}}$=$\frac{65}{6}$.
故选:D.
点评 本题考查了平面向量在立体几何中的应用,求出棱锥的高是关键,属于中档题.

| A. | 圆 | B. | 一个点 | C. | 两条直线 | D. | 不表示任何图形 |

| A. | 6 | B. | 9 | C. | 7 | D. | 2 |
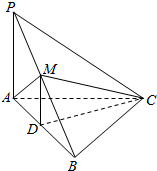 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.