题目内容
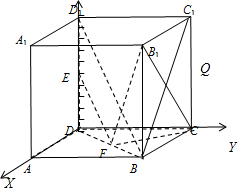
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为DD1的中点
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为DD1的中点(1)求证:BD1∥平面AEC
(2)求证:平面D1DB⊥平面AEC
(3)若P为对角线D1B的中点,Q为棱C1C上的动点求|PQ|的最小值.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,转化思想,空间位置关系与距离,空间向量及应用
分析:(1)连接BD交AC于F,连EF.可证EF∥D1B,又EF?平面EAC,从而可求得BD1∥平面EAC.
(2)先证明AC⊥BD,有DD1⊥平面ABCD,又AC?平面ABCD,可证明DD1⊥AC,从而可证AC⊥平面D1DB,即证明平面D1DB⊥平面AEC;
(3)以点D为坐标原点,以DA方向为x轴,DC方向为y轴,DD1方向为z轴,建立空间直角坐标系,先求出D1(0,0,2),B(2,2,0),C(0,2,0),再求出D1B的中点P(1,1,1),Q(0,2,z),从而可得PQ=
,可得当z=1时(此时Q为棱C1C的中点),PQmin=
.
(2)先证明AC⊥BD,有DD1⊥平面ABCD,又AC?平面ABCD,可证明DD1⊥AC,从而可证AC⊥平面D1DB,即证明平面D1DB⊥平面AEC;
(3)以点D为坐标原点,以DA方向为x轴,DC方向为y轴,DD1方向为z轴,建立空间直角坐标系,先求出D1(0,0,2),B(2,2,0),C(0,2,0),再求出D1B的中点P(1,1,1),Q(0,2,z),从而可得PQ=
| 2+(z-1)2 |
| 2 |
解答:
 (1)证明:连接BD交AC于F,连EF,
(1)证明:连接BD交AC于F,连EF,
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点,
在DDD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B,
又EF?平面EAC,所以BD1∥平面EAC.
(2)证明:在正方体ABCD-A1B1C1D1中,
∵四边形ABCD是正方形,∴AC⊥BD …5分
又在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面ABCD,…6分
又AC?平面ABCD,∴DD1⊥AC,…7分
DD1?平面D1DB,BD?平面D1DB,BD∩DD1=D,…8分
∴AC⊥平面D1DB …9分
∵AC?平面AEC,
∴平面D1DB⊥平面AEC …10分
(3)解:以点D为坐标原点,以DA方向为x轴,DC方向为y轴,DD1方向为z轴,建立空间直角坐标系,…11分
由正方体的棱长为2,知D1(0,0,2),B(2,2,0),C(0,2,0),
则D1B的中点P(1,1,1),Q(0,2,z)…12分
PQ=
,…13分
∴当z=1时(此时Q为棱C1C的中点),PQmin=
…14分
 (1)证明:连接BD交AC于F,连EF,
(1)证明:连接BD交AC于F,连EF,因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点,
在DDD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B,
又EF?平面EAC,所以BD1∥平面EAC.
(2)证明:在正方体ABCD-A1B1C1D1中,
∵四边形ABCD是正方形,∴AC⊥BD …5分
又在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面ABCD,…6分
又AC?平面ABCD,∴DD1⊥AC,…7分
DD1?平面D1DB,BD?平面D1DB,BD∩DD1=D,…8分
∴AC⊥平面D1DB …9分
∵AC?平面AEC,
∴平面D1DB⊥平面AEC …10分
(3)解:以点D为坐标原点,以DA方向为x轴,DC方向为y轴,DD1方向为z轴,建立空间直角坐标系,…11分
由正方体的棱长为2,知D1(0,0,2),B(2,2,0),C(0,2,0),
则D1B的中点P(1,1,1),Q(0,2,z)…12分
PQ=
| 2+(z-1)2 |
∴当z=1时(此时Q为棱C1C的中点),PQmin=
| 2 |
点评:本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,空间向量及应用,考查了转化思想,综合性较强,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(2,1)+f(1,2)=( )
| A、45 | B、60 | C、96 | D、108 |
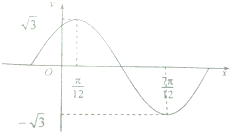 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< 如图,正方体ABCD-A1B1C1D1的棱长为2.
如图,正方体ABCD-A1B1C1D1的棱长为2.