题目内容
已知在数列{an}中,an>0,Sn是它前n项的和,且4Sn=(an+1)2,则数列{an}的通项公式an= .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知得(an+an-1)(an-an-1-2)=0,从而an-an-1=2,又4S1=4a1=(a1+1)2,解得a1=1,由此能求出an.
解答:
解:∵在数列{an}中,an>0,Sn是它前n项的和,
且4Sn=(an+1)2=an2+2an+1,①
∴4Sn-1=an-12+2an-1+1,②
①-②,得:an2-an-12-2(an+an-1)=0
∴(an+an-1)(an-an-1-2)=0,
∴an-an-1=2,
又4S1=4a1=(a1+1)2,解得a1=1,
∴数列{an}是首项为1,公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
故答案为:2n-1.
且4Sn=(an+1)2=an2+2an+1,①
∴4Sn-1=an-12+2an-1+1,②
①-②,得:an2-an-12-2(an+an-1)=0
∴(an+an-1)(an-an-1-2)=0,
∴an-an-1=2,
又4S1=4a1=(a1+1)2,解得a1=1,
∴数列{an}是首项为1,公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
故答案为:2n-1.
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足下列三个条件:
①对任意的x∈R,都有f(x+4)=f(x);
②对任意的0≤x1<x2≤2,都有f(x1)<f(x2);
③y=f(x+2)的图象关于y轴对称,
则下列结论中,正确的是( )
①对任意的x∈R,都有f(x+4)=f(x);
②对任意的0≤x1<x2≤2,都有f(x1)<f(x2);
③y=f(x+2)的图象关于y轴对称,
则下列结论中,正确的是( )
| A、f(7)<f(4.5)<f(6.5) |
| B、f(7)<f(6.5)<f(4.5) |
| C、f(4.5)<f(6.5)<f(7) |
| D、f(4.5)<f(7)<f(6.5) |
函数y=3
的值域为( )
| 1 |
| x-1 |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、{x|x≠1} |
| D、(1,+∞) |
不等式x2-3x+2<0的解集是( )
| A、{x|x<-2或x>-1} |
| B、{x|x<1或x>2} |
| C、{x|1<x<2} |
| D、{x|-2<x-1} |
定义在R上的偶函数,f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x1-x2)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
| A、f(-n)<f(n-1)<f(n+1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(n+1)<f(-n)<f(n-1) |
| D、f(n+1)<f(n-1)<f(-n) |
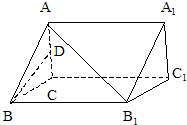 在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=
在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=