题目内容
1.已知随机变量ξ的分布列为:| ξ | -1 | 0 | 1 | 2 |
| P | x | $\frac{1}{3}$ | $\frac{1}{6}$ | y |
分析 由题意可得:x+y+$\frac{1}{3}+\frac{1}{6}$=1,-1×x+0+1×$\frac{1}{6}$+2y=$\frac{1}{3}$,解得x,y.再利用D(ξ)计算公式即可得出.
解答 解:由题意可得:x+y+$\frac{1}{3}+\frac{1}{6}$=1,-1×x+0+1×$\frac{1}{6}$+2y=$\frac{1}{3}$,
解得x=$\frac{5}{18}$,y=$\frac{2}{9}$.
∴D(ξ)=$(-1-\frac{1}{3})^{2}$×$\frac{5}{18}$+$(0-\frac{1}{3})^{2}$×$\frac{1}{3}$+$(1-\frac{1}{3})^{2}$×$\frac{1}{6}$+$(2-\frac{1}{3})^{2}×\frac{2}{9}$=$\frac{11}{9}$.
故答案为:$\frac{1}{2}$,$\frac{11}{9}$
点评 本题考查了随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列选项中,说法正确的是( )
| A. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| B. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| C. | 命题“若a=-b,则|a|=|b|”的否命题是真命题 | |
| D. | 命题“若$\left\{{\overrightarrow a,\overrightarrow b,\overrightarrow c}\right\}$为空间的一个基底,则$\left\{{\overrightarrow a+\overrightarrow b,\overrightarrow b+\overrightarrow c,\overrightarrow c+\overrightarrow a}\right\}$构成空间的另一个基底”的逆否命题为真命题 |
10.经过点A(-1,4)且在x轴上的截距为3的直线方程是( )
| A. | x+y+3=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y-3=0 |
11.设集合Sn={1,2,3,…2n-1},若X是Sn的子集,把X的所有元素的乘积叫做X的容量(规定空集的容量为0),若X的容量为奇(偶)数,则称X为Sn的奇(偶)子集.其中Sn的奇子集的个数为( )
| A. | $\frac{{{n^2}+n}}{2}$ | B. | 2n-1 | C. | 2n | D. | 22n-1-2n+1 |
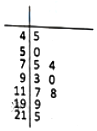 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士当地某年的AQI记录数据中,随机抽取10个,用茎叶图记录如图.根据该统计数据,估计此地该年AQI大于100的天数约为为146.(该年为365天)
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士当地某年的AQI记录数据中,随机抽取10个,用茎叶图记录如图.根据该统计数据,估计此地该年AQI大于100的天数约为为146.(该年为365天)