题目内容
对a、b∈R,记max{a, b}=
,设f1(x)=|x-1|,f2(x)=-x2+6x-5,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )
|
| A、[1,+∞) | ||
B、[
| ||
C、[
| ||
| D、(3,4) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由题意可得当|x-1|≥-x2+6x-5时,g(x)=|x-1|,当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,据此可作出函数g(x)和y=a的图象,数形结合可得结论.
解答:
解:由题意可知当|x-1|≥-x2+6x-5时,g(x)=|x-1|,
当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,
作出函数g(x)和y=a的图象如下:
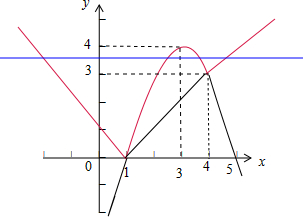
其中红色线为g(x)的图象,由图可知当a∈(3,4)时,
直线y=a和函数g(x)有4个不同的公共点,
故方程g(x)=a有四个不同的实数解,
故选:D.
当|x-1|<-x2+6x-5时,g(x)=-x2+6x-5,
作出函数g(x)和y=a的图象如下:

其中红色线为g(x)的图象,由图可知当a∈(3,4)时,
直线y=a和函数g(x)有4个不同的公共点,
故方程g(x)=a有四个不同的实数解,
故选:D.
点评:本题考查根的存在性和个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
根据如图的流程图,则输出的结果是( )


| A、7 | B、8 | C、720 | D、5040 |
根据条件:a、b、c满足c<b<a,且a+b+c=0,有如下推理:
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
| A、(1)(2) |
| B、(3)(4) |
| C、(1)(3) |
| D、(2)(4) |
下列选项中,p是q的必要不充分条件的是( )
A、p:f(x)=x3+2x2+mx+1在R上单调递增;q:m≥
| ||
| B、p:x=1;q:x=x2 | ||
| C、p:a+bi(a,b∈R)是纯虚数;q:a=0 | ||
| D、p:a+c>b+d;q:a>b且c>d |
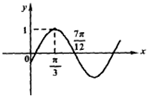 已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知导函数f′(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍,再向右平移
| ||||
C、先把各点的横坐标缩短到原来的
| ||||
D、先把各点的横坐标伸长到原来的2倍,再向左平移
|
数列2,5,8,11,…,则23是这个数列的( )
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
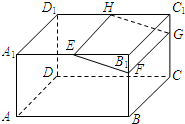 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )