题目内容
与方程
-
=2等价的方程是( )
| (x+2)2+y2 |
| (x-2)2+y2 |
A、x2-
| ||
B、x2-
| ||
C、y2-
| ||
D、x2-
|
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:利用两点间的距离公式和双曲线的定义求解.
解答:
解:由两点间距离公式知:
方程
-
=2表示动点(x,y)到定点(-2,0)和(2,0)
的距离之差为2,
∴动点(x,y)是以(-2,0),(2,0)为焦点,以2为实轴的双曲线的右支,
∴与方程
-
=2等价的方程是x2-
=1(x>0).
故选:A.
方程
| (x+2)2+y2 |
| (x-2)2+y2 |
的距离之差为2,
∴动点(x,y)是以(-2,0),(2,0)为焦点,以2为实轴的双曲线的右支,
∴与方程
| (x+2)2+y2 |
| (x-2)2+y2 |
| y2 |
| 3 |
故选:A.
点评:本题考查双曲线的定义的应用,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
根据条件:a、b、c满足c<b<a,且a+b+c=0,有如下推理:
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
| A、(1)(2) |
| B、(3)(4) |
| C、(1)(3) |
| D、(2)(4) |
反证法的关键是在正确的推理下得出矛盾,这个矛盾可以是( )
①与已知条件矛盾;
②与假设矛盾;
③与所证结论矛盾;
④与定义、定理、公理、法则矛盾;
⑤与事实矛盾.
①与已知条件矛盾;
②与假设矛盾;
③与所证结论矛盾;
④与定义、定理、公理、法则矛盾;
⑤与事实矛盾.
| A、①③④⑤ | B、①②④⑤ |
| C、①②③⑤ | D、①②③④ |
在数学归纳法证明“1+a+a2+…+an=
(a≠1,n∈N*)”时,验证当n=1时,等式的左边为( )
| 1-an+1 |
| 1-a |
| A、1 |
| B、1-a |
| C、1+a |
| D、1-a2 |
已知某个几何体的三视图如图所示,根据图中数据,求这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
| D、2 |
数列2,5,8,11,…,则23是这个数列的( )
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
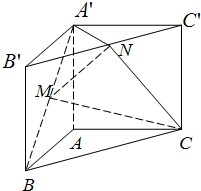 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=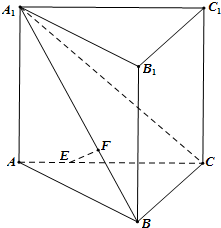 如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.
如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.