题目内容

把5名新兵分配到一、二、三3个不同的班，要求每班至少有一名且甲必须分配在一班，则所有不同的分配种数为
 
．
考点：排列、组合的实际应用
专题：计算题
分析：根据题意，分析可得一班最少有甲1人，最多可以有3人；则由此分3种情况讨论：①、若一班只有甲1人，②、一班有2人，③、一班有3人，分别求出每种情况下的分配方法数目，由分类计数原理计算可得答案．
解答： 解：根据题意，分3种情况讨论，
①、若一班只有甲1人，则二班可能有1人、2人、3人，共3种情况，
此时，有C41+C42+C43=14种分配方法；
②、若一班有2人，则二班可能有1人、2人，共2种情况，
此时，有C41×[C31+C32]=24种分配方法；
③、若一班有3人，则二班、三班各有1人，
此时有C42×C21=12种分配方法，
综上，不同的分配方法共有14+24+12=50种
故答案为50．
点评：本题考查排列、组合的应用，解题时注意要分析一班的人数可能情况，由此进行分类讨论．
练习册系列答案
相关题目
已知函数f（x）=-x3+x2+b，g（x）=alnx．
（1）若f（x）的极大值为
4
27
，求实数b的值；
（2）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求实数a的取值范围；
（3）若函数f（x）满足：在定义域内存在实数x0，使f（x0+k）=f（x0）+f（k）（k为常数），则称“f（x）关于k可线性分解”．设b=0，若F（x）=
af(x)
x2
+g（x）关于实数a可线性分解，求a取值范围．
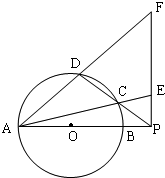如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P做AP的垂线，交直线AC于点E，交直线AD于点F．
（1）求证：∠PEC=∠PDF；
（2）求PE•PF的值．
已知实数a1，a2，a3不全为零，正数x，y满足x+y=2，设
xa1a2+ya2a3
a12+a22+a32
的最大值为M=f（x，y），则M的最小值为
 
．
过原点的直线l与函数y=
1
x
的图象交于B，C两点，A为抛物线x2=-8y的焦点，则|
AB
+
AC
|=
 
．
以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，已知点P在曲线
x=1+cosα
y=sinα
（α为参数）上，点Q在直线ρ=
3
2
sin(θ+
π
4
)
上，则|PQ|的最小值是
 
．
已知中心在原点，坐标轴为对称轴的双曲线的渐近线方程是y=±4x，则该双曲线的离心率是
 
．
已知a、b、c分别为△ABC三个内角A、B、C的对边，若（c-b）sinC=asinA-bsinB，则∠A=
 
．
设x、y、z是正数，且x2+4y2+9z2=4，2x+4y+3z=6，则x+y+z等于（　　）
A、
20
9
B、
11
5
C、
6
5
D、
11
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网