题目内容
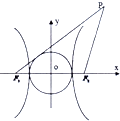 如图,点P在双曲线
如图,点P在双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设PF1与圆相切于点M,利用|PF2|=|F1F2|,及直线PF1与圆x2+y2=a2相切,可得几何量之间的关系,从而可求双曲线的离心率的值.
解答:
解:设PF1与圆相切于点M,因为|PF2|=|F1F2|,所以△PF1F2为等腰三角形,
所以|F1M|=
|PF1|,
又因为在直角△F1MO中,|F1M|2=|F1O|2-a2=c2-a2,所以|F1M|=b=
|PF1|①
又|PF1|=|PF2|+2a=2c+2a ②,
c2=a2+b2 ③
由①②③解得
=
.
故选:B.
所以|F1M|=
| 1 |
| 4 |
又因为在直角△F1MO中,|F1M|2=|F1O|2-a2=c2-a2,所以|F1M|=b=
| 1 |
| 4 |
又|PF1|=|PF2|+2a=2c+2a ②,
c2=a2+b2 ③
由①②③解得
| c |
| a |
| 5 |
| 3 |
故选:B.
点评:本题考查直线与圆相切,考查双曲线的定义,考查双曲线的几何性质,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
设集合A={x|1<x<5},B={x|x2-2x-3≤0},则A∩(∁RB)=( )
| A、(1,5) |
| B、(3,5) |
| C、(1,3) |
| D、(1,2) |
平面区域
的面积是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
,
满足|
|=2|
|,
-
与2
+
的夹角为
,则
,
的夹角是( )
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
| π |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
设x、y、z是正数,且x2+4y2+9z2=4,2x+4y+3z=6,则x+y+z等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={x|x≤6,x∈N},B={x|x-3>0,x∈R},则A∩B=( )
| A、{4,5,6} |
| B、{0,4,5,6} |
| C、{3,4,5,6} |
| D、∅ |
已知a:b:c=1:2:4,则双曲线ax2-by2=c的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|