题目内容
方程3x+1-x=6的解所在的区间是（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由方程可得3x+1-x-6=0，设函数f（x）=3x+1-x-6，则根据函数零点的判定讨论，即可得到结论．
解答：
解：设函数f（x）=3x+1-x-6，
则f（0）=3-0-6=-3＜0，
f（1）=32-1-6=9-7=2＞0，
则f（0）f（1）＜0，即函数f（x）零点所在的区间为（0，1），
则方程3x+1-x=6的解所在的区间为（0，1），
故选：A．
则f（0）=3-0-6=-3＜0，
f（1）=32-1-6=9-7=2＞0，
则f（0）f（1）＜0，即函数f（x）零点所在的区间为（0，1），
则方程3x+1-x=6的解所在的区间为（0，1），
故选：A．
点评：本题主要考查函数零点区间的判定，利用方程和函数的关系，结合函数零点存在的判定条件是解决本题的关键．
练习册系列答案
相关题目
设x、y、z是正数，且x2+4y2+9z2=4，2x+4y+3z=6，则x+y+z等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
与双曲线2y2-x2=4焦距不同的是（ ）
| A、2x2-y2=4 |
| B、y2-x2=3 |
| C、x2+4y2=8 |
| D、2y2+x2=6 |
已知a：b：c=1：2：4，则双曲线ax2-by2=c的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设i是虚数单位，
是复数z=
+
i的共轭复数，则z2•
=（ ）
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
已知
=1-i，其中x，y∈R，i为虚数单位，则x+yi=（ ）
| x |
| 1+yi |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
已知函数f（x）是定义在R上的奇函数，对任意x，y∈R，x+y≠0，都有
＞0，若x＞2y，则（ ）
| f(x)+f(y) |
| x+y |
| A、f（x）＞f（2y） |
| B、f（x）≥f（2y） |
| C、f（x）＜f（2y） |
| D、f（x）≤f（2y） |
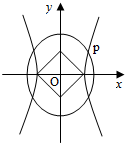如图，O为坐标原点，双曲线C1：