题目内容
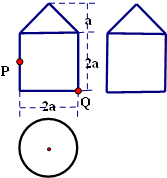 一个几何体的三视图及部分度量值如图所示,其中,正视图与侧视图都是由一个正方形和一个等腰三角形组成,俯视图是一个圆.
一个几何体的三视图及部分度量值如图所示,其中,正视图与侧视图都是由一个正方形和一个等腰三角形组成,俯视图是一个圆.(1)判断该几何体的结构特征,并求其表面积;
(2)如果正视图中的点P是其所在线段的中点,点Q是其所在正方形的顶点,试求:在原几何体的侧面上,从P点到Q点的最短路径的长.
考点:多面体和旋转体表面上的最短距离问题,由三视图求面积、体积
专题:空间位置关系与距离
分析:(1)由三视图知:该几何体是一个圆锥加上一个同底圆柱,分别求出圆锥、圆柱的高和底面半径,代入表面积公式,可得答案;
(2)沿P点所在母线和Q点所在母线剪开圆柱,展开得圆柱的半个侧面,利用勾股定理可得从P点到Q点的最短路径的长.
(2)沿P点所在母线和Q点所在母线剪开圆柱,展开得圆柱的半个侧面,利用勾股定理可得从P点到Q点的最短路径的长.
解答:
解:(1)由三视图知:该几何体是一个圆锥加上一个同底圆柱,
且圆锥、圆柱的高分别为a,2a,底面半径为a,…(3分)
所以此几何体表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和,
∴S=
×(2πa)×
a+(2πa)×2a+4πa2=(
+5)πa2,…(8分)
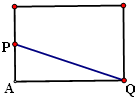
(2)沿P点所在母线和Q点所在母线剪开圆柱,展开得圆柱的半个侧面,
如图所示,
 ,
,
则PQ=
=
=
a,
∴在原几何体的侧面上,从P点到Q点的最短路径的长为
a.…(12分)
且圆锥、圆柱的高分别为a,2a,底面半径为a,…(3分)
所以此几何体表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和,
∴S=
| 1 |
| 2 |
| 2 |
| 2 |
(2)沿P点所在母线和Q点所在母线剪开圆柱,展开得圆柱的半个侧面,
如图所示,
 ,
,则PQ=
| AP2+AQ2 |
| a2+(πa)2 |
| 1+π2 |
∴在原几何体的侧面上,从P点到Q点的最短路径的长为
| 1+π2 |
点评:本题考查的知识点是旋转体表面上的最短距离问题,由三视图求面积,体积,难度不大,属于基础题.

练习册系列答案
相关题目
如果有下列这段伪代码,那么将执行多少次循环( )


| A、4次 | B、5次 | C、7次 | D、10次 |
已知函数f(x)=
若f(f(0))≥a2-1,则实数a的取值范围为( )
|
| A、[3,4] |
| B、[2,3] |
| C、[1,2] |
| D、[-1,2] |
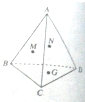 如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.
如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.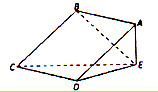 如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,
如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,