题目内容
函数f(x)=x-ex的零点个数为 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由f(x)=x-ex=0得x=ex,分别作出函数y=x和y=ex的图象,即可得到结论.
解答:
 解:由f(x)=x-ex=0得x=ex,分别作出函数y=x和y=ex的图象,
解:由f(x)=x-ex=0得x=ex,分别作出函数y=x和y=ex的图象,
由图象可知两个图象有0个不同的交点,
即函数f(x)的零点个数为0,
故答案为:0
 解:由f(x)=x-ex=0得x=ex,分别作出函数y=x和y=ex的图象,
解:由f(x)=x-ex=0得x=ex,分别作出函数y=x和y=ex的图象,由图象可知两个图象有0个不同的交点,
即函数f(x)的零点个数为0,
故答案为:0
点评:本题考查函数与方程问题,求解此类问题的基本方法是令f(x)=0,将函数分解为两个基本初等函数,然后在同一坐标系下,作出两函数的图象,则两函数图象的交点个数,即为函数零点的个数.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知等比数列{an}的前n项和为Sn,a1+a3+a5-(a2+a4)=8,a12+a32+a52+(a22+a42)=12,则S5=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
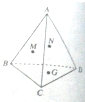 如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.
如图,已知A为平面BCD外一点,M,N,G分别是△ABC、△ABD、△BCD的重心,求证:平面MNG∥平面ACD.