题目内容
椭圆的中心是原点O,它的长轴长为2a,短轴长为2
,右焦点为F(c,0)(c>0),设点A(
,0),|OF|=2|FA|,过点A的直线与椭圆相交于P,Q两点
(1)求椭圆的方程及离心率;
(2)若
•
=0,求直线PQ的方程;
(3)设
=λ
(λ>1),过点P作x轴的垂线与椭圆相交于另一点M,证明
=-λ
.
| 2 |
| a2 |
| c |
(1)求椭圆的方程及离心率;
(2)若
. |
| OP |
. |
| OQ |
(3)设
. |
| AP |
. |
| AQ |
. |
| FM |
. |
| FQ |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆的方程为
+
=1,a>
.列出关于a,b的方程组,解出a,b值,从而求得椭圆的方程及离心率.
(2)由(1)可得A(3,0).设直线PQ的方程为y=k(x-3).将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直条件即可求得k值,从而解决问题.
(3)先得出向量的坐标
=(x1-3,y1),
=(x2-3,y2),由已知得方程组解得x2,最后经计算得出
=-λ
即可.
| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
(2)由(1)可得A(3,0).设直线PQ的方程为y=k(x-3).将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直条件即可求得k值,从而解决问题.
(3)先得出向量的坐标
| AP |
| AQ |
. |
| FM |
. |
| FQ |
解答:
(1)解:由题意,可设椭圆的方程为
+
=1,a>
.
由已知得
,解得a=
,c=2,
所以椭圆的方程为
+
=1,离心率e=
.
(2)解:由(1)可得A(3,0).
设直线PQ的方程为y=k(x-3).
由方程组
,得(3k2+1)x2-18k2x+27k2-6=0,
依题意△=12(2-3k2)>0,得-
<k<
.
设P(x1,y1),Q(x2,y2),则x1+x2=
,①
x1x2=
.②
由直线PQ的方程得y1=k(x1-3),y2=k(x2-3).
于是y1y2=k2(x1-3)(x2-3)=k2[x1x2-3(x1+x2)+9].③
∵
•
=0,∴x1x2+y1y2=0.④
由①②③④得5k2=1,∴5k2=1.∴k=±
∈(-
,
),
∴直线PQ的方程为x-
y-3=0或x+
y-3=0.
(3)证明:
=(x1-3,y1),
=(x2-3,y2),
由已知得方程组
.
注意λ>1,解得x2=
,
∵F(2,0),M(x1,-y1),
∴
=(x1-2,-y1)=(λ(x2-3)+1,-y1)
=(
,-y1)=-λ(
,y2),
∵
=(x2-2,y2)=(
,y2),
∴
=-λ
.
| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
由已知得
|
| 6 |
所以椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
| ||
| 3 |
(2)解:由(1)可得A(3,0).
设直线PQ的方程为y=k(x-3).
由方程组
|
依题意△=12(2-3k2)>0,得-
| ||
| 3 |
| ||
| 3 |
设P(x1,y1),Q(x2,y2),则x1+x2=
| 18k2 |
| 3k2+1 |
x1x2=
| 27k2-6 |
| 3k2+1 |
由直线PQ的方程得y1=k(x1-3),y2=k(x2-3).
于是y1y2=k2(x1-3)(x2-3)=k2[x1x2-3(x1+x2)+9].③
∵
| OP |
| OQ |
由①②③④得5k2=1,∴5k2=1.∴k=±
| ||
| 5 |
| ||
| 3 |
| ||
| 3 |
∴直线PQ的方程为x-
| 5 |
| 5 |
(3)证明:
| AP |
| AQ |
由已知得方程组
|
注意λ>1,解得x2=
| 5λ-1 |
| 2λ |
∵F(2,0),M(x1,-y1),
∴
| FM |
=(
| 1-λ |
| 2 |
| λ-1 |
| 2λ |
∵
| FQ |
| λ-1 |
| 2λ |
∴
| FM |
| FQ |
点评:本题主要考查椭圆的标准方程和几何性质,直线方程,平面向量的计算,曲线和方程的关系等解析几何的基本思想方法和综合解题能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
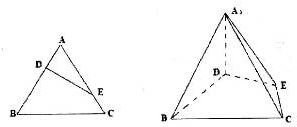 已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足
已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足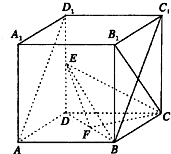 如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.
如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.